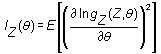Estimadores eficientes
Sea 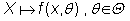 una
población, una
población, 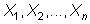 una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Si una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Si 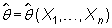 es
un estimador insesgado de q, cuya varianza
alcanza la cota de Cramér-Rao, esto es, tal que es
un estimador insesgado de q, cuya varianza
alcanza la cota de Cramér-Rao, esto es, tal que
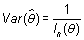
recibe el nombre de estimador eficiente.
Obviamente, todo estimador
eficiente es insesgado de mínima varianza, y el recíproco no es cierto.
La cantidad 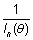 recibe
el nombre de cota de Cramér-Rao. recibe
el nombre de cota de Cramér-Rao.
|
En definitiva, existen varias situaciones posibles:
- No se cumplen las condiciones de regularidad de Cramér-Rao.
En esta situación, si existe un estimador insesgado de mínima varianza, no
tenemos ninguna forma de obtenerlo, ni de comprobar si lo es un estimador
propuesto.
- Se cumplen las condiciones de regularidad de Cramér-Rao,
pero ningún estimador insesgado alcanza la cota de Cramér-Rao. Como en
la situación anterior, si existe un estimador insesgado de mínima
varianza, no tenemos ninguna forma de obtenerlo, ni de comprobar si lo es
un estimador propuesto.
- Se cumplen las condiciones de regularidad de Cramér-Rao,
y un estimador insesgado alcanza la cota de Cramér-Rao. Entonces es el
(único) estimador insesgado de mínima varianza.
Desde el punto de vista práctico, en las situaciones segunda
y tercera, es muy diferente comprobar si
un estimador propuesto es eficiente y obtener un
estimador eficiente. Para comprobar si un estimador propuesto es eficiente,
basta con estudiar si es insesgado y, si lo es, calcular su varianza y compararla
con la cota de Cramér-Rao. Pero, para obtener un estimador eficiente, la definición
nos indica que debiéramos probar con distintos estimadores en la esperanza
de que alguno de ellos sea insesgado y su varianza alcance la cota, tarea harto
penosa y, posiblemente estéril, ya que existen infinitos estimadores de un
parámetro. El siguiente teorema, que no demostraremos, proporciona una forma
de obtener un estimador eficiente, cuando exista.
-
T es un estimador eficiente de q.
-
 , donde 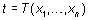 es
una estimación de q.
-
T es suficiente para q, y además, si 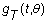 es
la función de densidad de T, se cumple
|
Este resultado se utiliza fundamentalmente en la dirección  .
En concreto, para un problema para el que se cumplan las condiciones de regularidad,
se intenta realizar la descomposición de la segunda condición. Si es posible,
obtendremos una función
.
En concreto, para un problema para el que se cumplan las condiciones de regularidad,
se intenta realizar la descomposición de la segunda condición. Si es posible,
obtendremos una función 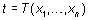 de
la realización de la muestra, que nos sugiere un candidato,
de
la realización de la muestra, que nos sugiere un candidato, 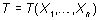 a
estimador eficiente. Se calcula entonces su esperanza y, si E[T] = q,
T es insesgado, con lo que la equivalencia anterior es aplicable y se cumplirá
la primera condición,
esto es, T será eficiente.
a
estimador eficiente. Se calcula entonces su esperanza y, si E[T] = q,
T es insesgado, con lo que la equivalencia anterior es aplicable y se cumplirá
la primera condición,
esto es, T será eficiente.
El resultado anterior se utiliza también en la dirección 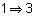 ,
que garantiza que todo estimador eficiente es además suficiente.
,
que garantiza que todo estimador eficiente es además suficiente.
Finalmente, la descomposición que proporciona el resultado
segundo no sólo permite obtener, si existe, un estimador eficiente, sino que
suministra su varianza, que puede ser compara con la de otros estimadores insesgados.
En concreto, si existe un estimador eficiente, 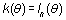 ,
esto es, k(q) es la cantidad de información de la muestra, y por tanto,
,
esto es, k(q) es la cantidad de información de la muestra, y por tanto,
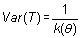
Cantidad de información de Fisher
Anteriormente, hemos denominado cantidad de información de
la muestra al denominador de la cota de Cramér-Rao,
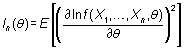
Esta cantidad podría necesitarse en relación con la cota
de Cramér-Rao (es su inversa) y, por tanto, para la obtención de estimadores
eficientes. No obstante, hemos señalado que para buscar estimadores eficientes
sólo es necesario realizar la descomposición propuesta en el anterior resultado
para la parcial del neperiano de la función de densidad de la muestra. Más
aún, dicha descomposición proporciona directamente la cantidad de información
de la muestra, ya que 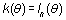 .
.
Por tanto, con nuestros objetivos de trabajo, no es necesario
manejar con soltura dicha cantidad de información. No obstante, algunas ideas
y resultados básicos pueden ser de interés para los lectores que se planteen
profundizar en este concepto. Los describiremos esquemáticamente:
1. El concepto: Cuando la distribución de
probabilidades de una variable aleatoria, Z, depende de un parámetro
q, se dice que la variable Z tiene información sobre
el parámetro. Si, por concretar el comentario, suponemos a partir de ahora
que la variable es continua, y llamamos 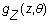 a
su función de densidad, la derivada
a
su función de densidad, la derivada

será distinta de cero porque el numerador lo es, y podemos
calcular la esperanza de su cuadrado, que será habitualmente distinta de cero,
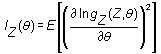
Se dice que esta esperanza es la cantidad
de información de Z (de su función de densidad) sobre
q. Obsérvese que esta cantidad
será mayor cuanto más varíe la función de densidad de Z al cambiar el parámetro,
esto es, cuanto más dependa 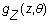 de
q.
de
q.
2. Ayudas al cálculo:
Cuando se derivan los neperianos de las densidades, todos los sumandos que
no dependen del parámetro tienen derivada igual a cero. Por ello la facilidad
de cálculo aumenta con el orden de derivación. El siguiente resultado es útil
si es necesario obtener directamente la cantidad de información:
Sea 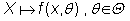 una
población, una
población, 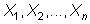 una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Entonces, una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Entonces,

puede calcularse como

|
3. Población y muestras:
Supongamos que tenemos una población, 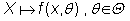 ,
y tomamos una muestra aleatoria simple,
,
y tomamos una muestra aleatoria simple, 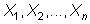 ,
de X. Entonces, si se cumplen las condiciones de regularidad de Cramér-Rao,
la cantidad de información es acumulativa, esto es, una muestra de tamaño 8
tiene el doble de información sobre q que
una de tamaño 4. El siguiente recuadro formaliza este resultado:
,
de X. Entonces, si se cumplen las condiciones de regularidad de Cramér-Rao,
la cantidad de información es acumulativa, esto es, una muestra de tamaño 8
tiene el doble de información sobre q que
una de tamaño 4. El siguiente recuadro formaliza este resultado:
Sea 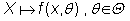 una
población, una
población, 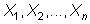 una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Entonces, si llamamos una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Entonces, si llamamos
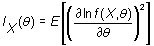
a la cantidad de información de la población y

la de la muestra, se cumple  . .
|
4. Muestras y estadísticos: Los estadísticos
son resúmenes de las muestras y, por tanto, no pueden tener más información
que ellas sobre el parámetro.
Veamos el siguiente resultado:
![]() una
población,
una
población, ![]() una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Si
una
m.a.s. de X. Supongamos que se cumplen las condiciones de regularidad
de Cramér-Rao. Si ![]() es
un estimador insesgado de q, cuya varianza
alcanza la cota de Cramér-Rao, esto es, tal que
es
un estimador insesgado de q, cuya varianza
alcanza la cota de Cramér-Rao, esto es, tal que ![]()
![]() recibe
el nombre de cota de Cramér-Rao.
recibe
el nombre de cota de Cramér-Rao.