Índices de precios, cantidades y valores
Los índices simples y complejos de mayor interés son los índices de precios, cantidades y valores.
1.1. Índices simples
Sea ![]() el
precio de un bien en el periodo t.
el
precio de un bien en el periodo t.
Índices de precios o precios relativos:
En la hoja adjunta se ilustra estos índices simples con datos sobre los precios percibidos por los agricultores (en euros por 100 Kg.) de tres tipos de cereales para España.
1.2. Índices complejos
Sean ![]() y
y ![]() el
precio y la cantidad del bien i-ésimo en el periodo t.
el
precio y la cantidad del bien i-ésimo en el periodo t.
1.2.1. Índices complejos sin ponderar
Índice de Sauerbeck: media aritmética de los índices simples del conjunto de bienes.
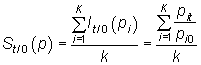 |
Índice de Bradstreet-Dûtot: media agregativa de los precios del conjunto de bienes.
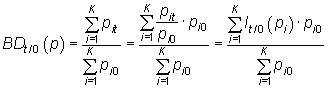 |
También se puede expresar como la media aritmética ponderada de los índices simples siendo las ponderaciones los precios de cada bien en el periodo base.
1.2.2. Índices complejos ponderados
Índice de Laspeyres: media agregativa de precios ponderados por las cantidades
del periodo base.
 |
Como se puede observar por la última
igualdad de la expresión
anterior, el índice de Laspeyres se puede expresar como una media aritmética
ponderada de índices simples de precios. La ponderación utilizada
es el valor de la cantidad producida (consumida) del bien i-ésimo
en el periodo base a precios de dicho periodo, ![]() .
Dada la importancia de este índice, en la hoja
adjunta se ilustra su cálculo con datos
sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y
las producciones (en miles de toneladas) de tres tipos de
cereales para España.
.
Dada la importancia de este índice, en la hoja
adjunta se ilustra su cálculo con datos
sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y
las producciones (en miles de toneladas) de tres tipos de
cereales para España.
Índice de Paasche: media agregativa de precios ponderados por las cantidades del periodo corriente.
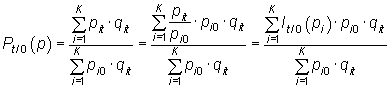 |
También el índice de Paasche
se puede expresar como media aritmética
ponderada de índices simples de precios. En este caso la ponderación
utilizada es el valor de la cantidad producida (consumida) del bien i-ésimo en
el periodo corriente a precios del periodo base, ![]() .
.
El cálculo de este último índice es más laborioso
porque exige una renovación de las ponderaciones en cada periodo.
Índice de Edgeworth: media agregativa de precios ponderados por la suma (la media) de las cantidades del periodo base y del periodo corriente.
 |
También
se puede expresar como media aritmética ponderada de índices
simples de precios, siendo la ponderación utilizada
el valor de la suma (la media) de las cantidades producidas (consumidas) del
bien i-ésimo en
el periodo base y en el corriente a precios del
periodo base, ![]() .
.
Índice de Fisher: media geométrica de los índices de Laspeyres y Paasche.
Los índices de Edgeworth y de Fisher son soluciones de compromiso entre los índices de Laspeyres y Paasche.
En la hoja adjunta se ilustran los índices de precios con datos sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y las producciones (en miles de toneladas) de tres tipos de cereales para España.
2.1. Índices simples
Sea ![]() la cantidad de un bien en el periodo t.
la cantidad de un bien en el periodo t.
Índices de cantidades o cantidades relativas:
En la hoja adjunta se ilustra estos índices simples con datos sobre producciones (en miles de toneladas) para España de tres tipos de cereales.
2.2. Índices complejos
Sean ![]() y
y ![]() el
precio y la cantidad del bien i-ésimo en el periodo t.
el
precio y la cantidad del bien i-ésimo en el periodo t.
2.2.1. Índices complejos sin ponderar
Índice de Sauerbeck: media aritmética de los índices
simples del conjunto de bienes.
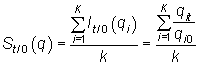 |
Índice de Bradstreet-Dûtot: media agregativa de las cantidades del conjunto de bienes.
 |
También se puede expresar como la media aritmética ponderada de los índices simples siendo las ponderaciones las cantidades de cada bien en el periodo base.
2.2.2. Índices complejos ponderados
Índice de Laspeyres: media agregativa de cantidades ponderadas por los
precios del periodo base.
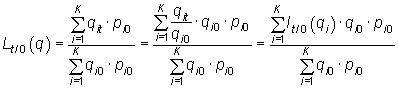 |
Como se puede observar por la última
igualdad de la expresión
anterior, el índice de Laspeyres se puede expresar como una media aritmética
ponderada de índices simples de cantidades. La ponderación utilizada
es la misma que para el índice de precios, es decir, el valor de la
cantidad producida (consumida) del bien i-ésimo en el periodo base a
precios de dicho periodo, ![]() .
.
Índice de Paasche: media agregativa de cantidades ponderadas por los
precios del periodo corriente.
 |
También el índice de Paasche
se puede expresar como media aritmética
ponderada de índices simples de cantidades. En este caso la ponderación
utilizada es el valor de la cantidad producida (consumida) del bien i-ésimo en
el periodo base
a precios del periodo corriente, ![]() .
.
Índice de Edgeworth: media agregativa de cantidades ponderadas por la suma (la media) de los precios del periodo base y del periodo corriente.
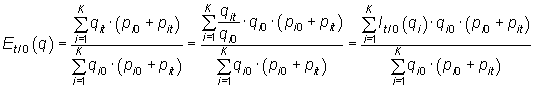 |
También se puede expresar como media
aritmética ponderada de índices simples de cantidades, siendo
la ponderación utilizada el valor de la cantidad del periodo base
del bien i-ésimo al precio resultante de la suma (la media)
de los precios en el periodo base
y en el corriente, ![]() .
.
Índice de Fisher: media geométrica de los índices
de Laspeyres y Paasche.
En la hoja adjunta se ilustran los índices de cantidades con datos sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y las producciones (en miles de toneladas) de tres tipos de cereales para España.
3.1. Índices simples
Sean ![]() y
y ![]() el
precio y la cantidad de un bien en el periodo t. El valor de un bien
en un período dado es el producto del precio de ese bien y de la cantidad
producida,
el
precio y la cantidad de un bien en el periodo t. El valor de un bien
en un período dado es el producto del precio de ese bien y de la cantidad
producida, ![]() ,
esto es, la cantidad valorada.
,
esto es, la cantidad valorada.
Índices de valores o valores relativos:
En la hoja adjunta se ilustra estos índices simples con datos sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y las producciones (en miles de toneladas) de tres tipos de cereales para España.
3.2. Índices complejos
Sean ![]() y
y ![]() el
precio y la cantidad del bien i-ésimo en el periodo t. Dado
que el valor de un bien en un periodo cualquiera es el producto del precio de
ese
bien
y la cantidad producida (vendida o
consumida), el valor del bien i-ésimo en el periodo t es
el
precio y la cantidad del bien i-ésimo en el periodo t. Dado
que el valor de un bien en un periodo cualquiera es el producto del precio de
ese
bien
y la cantidad producida (vendida o
consumida), el valor del bien i-ésimo en el periodo t es ![]() .
De la misma forma, el valor del conjunto de bienes será
.
De la misma forma, el valor del conjunto de bienes será
Al igual que los índices de precios y cantidades, el índice complejo de valor entre el periodo 0 y el periodo t es el cociente entre el valor del conjunto de bienes en el periodo t y el valor del conjunto de bienes en el periodo 0:
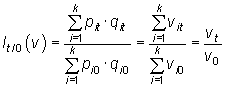 |
Como se observa en la última expresión, el índice complejo de valor es una media agregativa de los índices simples de valor.
El índice de valor se puede obtener a partir del producto de los índices de Laspeyres y de Paasche:
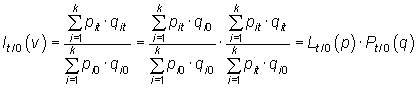 |
o bien,
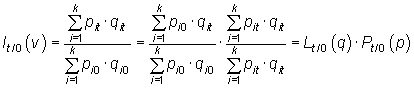 |
También el producto del índice de precios y el de cantidades de Fisher proporciona el índice de valor:
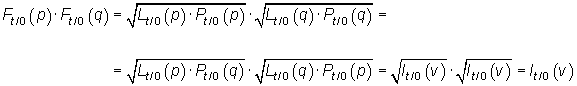 |
En la hoja adjunta se ilustran los índices de valor con datos sobre los precios percibidos por los agricultores (en euros por 100 Kg.) y las producciones (en miles de toneladas) de tres tipos de cereales para España.