Componentes de una serie temporal

Con bastante frecuencia, las series temporales presentan una o varias características, denominadas componentes, que ayudan a explicar su comportamiento en el tiempo. No es fácil dar una definición estricta de las mismas, pero aunque sea de manera amplia, una descripción de su significado puede ser conveniente:

Tendencia (componente tendencial)

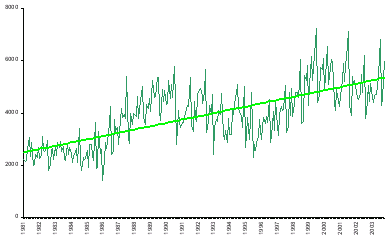
Se denomina tendencia de una serie temporal a su comportamiento o movimiento a largo plazo. Por ejemplo, la gráfica adjunta muestra la serie de ventas de turismos en Castilla y León desde enero de 1980. La línea recta podría representar la tendencia (creciente). La pendiente es de 10.4, lo que indica que "tendencialmente" cada mes se venden 10.4 turismos más que en el anterior.

Esa recta se ha construido como la recta de regresión de la nube de puntos que representa la serie y, como veremos, es una de las opciones a la hora de calcular la tendencia. Usaremos la notación o bien

Componente cíclica

Esta componente refleja comportamientos recurrentes, aunque no tienen por qué ser exactamente periódicos, con un periodo superior a un año. Muestran, habitualmente, cómo se suceden las etapas de bonanza económica con las de crisis, o al menos, desaceleración.

Con frecuencia los ciclos económicos resultan de la superposición o yuxtaposición de distintos efectos, con periodos diferentes, más cortos o más largos (dos años, diez o veinte años, etc.). Por ello, son difícilmente reconocibles. Por ello, muchas veces no se consiguen separar de la tendencia, al menos para series no demasiado largas. Denominaremos a la componente cíclica como o .

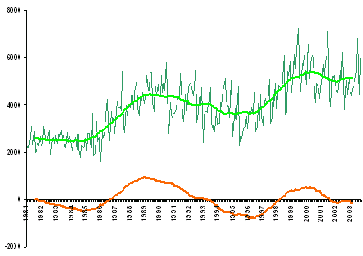
La figura de la derecha ilustra esta definición con la representación de la anterior serie de ventas de turismos, junto con la componente cíclica (de color naranja). Como decíamos, a veces no se separa de la tendencia. A la componente se le denomina entonces la "ciclo-tendencia". En esa figura se muestra (en color verde y con trazo grueso) la ciclo-tendencia de la serie de ventas de turismos.

No separaremos ciclo y tendencia en estos materiales, por lo que, siempre que nos refiramos a la tendencia, estaremos hablando, de hecho, de la ciclo-tendencia.

Componente estacional

Este es el motivo por el que se consideran los periodos agrupados en otros periodos más amplios en el tratamiento de muchas series temporales. Muchas series económicas presentan oscilaciones regulares en el mismo mes de cada año, y con unas pautas que se presentan, sin repetirse exactamente, todos los años. Son las llamadas "variaciones estacionales", y se deben básicamente a causas climatológicas, vacacionales o fiscales. Las denominaremos muy raramente con la notación y con frecuencia en la forma .

La figura adyacente muestra en un gráfico especial, de los denominados de "telaraña" las matriculaciones de turismos en Castilla y León durante los años 1999 a 2003. Cada radio es un mes (1 para enero, 2 para febrero, etc.) y puede observarse ciertas pautas. Por ejemplo, que enero, agosto y septiembre son meses con pocas matriculaciones relativas, mientras que julio y junio son meses de elevados valores, en comparación con la tendencia. No representamos más años en esta gráfica, pero el efecto no es muy diferente si lo hacemos.

La estacionalidad no se presenta sólo cuando el periodo amplio es el año. A veces hay estacionalidades mensuales o semanales en series diarias, o estacionalidades diarias en series horarias, como son las series de cotizaciones bursátiles, por ejemplo. Sí es importante que las estacionalidades tengan un periodo no superior al anual, para que no se confundan con las componentes cíclicas.

Supondremos en este trabajo que la componente estacional es exactamente periódica, esto es,

y que se cumple el denominado "principio de conservación de las áreas", que para el modelo aditivo indica que la media "anual" de las componentes estacionales es igual a cero, esto es,

Componente irregular

También llamado "ruido", recoge alteraciones de la serie, pequeñas en su incidencia, y sin una pauta periódica ni tendencial reconocible. Se considera que está ocasionada por múltiples factores, de pequeña entidad y diferentes ritmos temporales, que no se pueden estudiar individualmente. Esto en la teoría, porque en la práctica lo que ocurre es que la consideración de una serie como compuesta por componentes tendenciales, cíclicas y estacionales no deja de ser un modelo y, como tal, una representación aproximada e imperfecta, aunque valiosa, del mundo real. La componente irregular recogería, en consecuencia, la incapacidad del modelo para explicar a la perfección el comportamiento de la serie temporal.

Nótese que si se impone que no tengan pautas tendenciales o periódicas de la serie, deben entonces comportarse de forma independiente de las otras componentes, que tienen unas pautas sistemáticas.

Se describe como o .