Extracción de la tendencia

Los métodos más utilizados son dos: el ajuste analítico y el de medias móviles.

Método de ajuste analítico

Se ajustan los datos (la nube de puntos ) a una recta por el método de mínimos cuadrados. En concreto, se obtiene la tendencia como la recta , con

, .

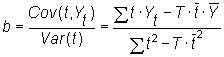Si hay suficientes datos, se ajustan las medias "anuales", esto es, la nube de puntos , donde

,

Aunque habitualmente el ajuste se hace a una recta, es conveniente observar previamente el aspecto de la serie (de su representación gráfica) por si fuese conveniente ajustar la nube a otro tipo de función o realizar previamente una transformación logarítmica de los datos.

La ventaja de este procedimiento sobre el de medias móviles reside en que se puede analizar la bondad del ajuste. Además, se pueden obtener valores de la tendencia para periodos que estén fuera del intervalo (1, T).

Presenta el problema de decidir el tipo de función adecuado o el grado del polinomio en t, especialmente para series de pequeña longitud.

Método de medias móviles

La definición es complicada analíticamente, pero muy simple en su utilización. Por ejemplo, la media móvil de orden 3 (o sea, con p=3) es la serie

y para la media móvil de orden cuatro (p=4) calculamos primero

y finalmente la media móvil se obtiene como

Nótese que las medias móviles de orden par pueden obtenerse en un solo paso. Por ejemplo

Éstas son medias móviles denominadas "ponderadas", entendido este calificativo en el sentido de que no todas las ponderaciones son iguales (a 1/p). Nótese que una media móvil de orden, p, par, es una media móvil ponderada de orden p+1, en la que los términos extremos tienen un peso igual a 1/(2p), y el resto un peso igual a 2/(2p). No nos dedicaremos en este trabajo a las medias móviles ponderadas, pero digamos que algunas de ellas son muy populares. Por ejemplo, se utiliza con frecuencia para extraer la ciclo-tendencia de series mensuales la denominada de Spencer, media móvil ponderada de 15 términos,

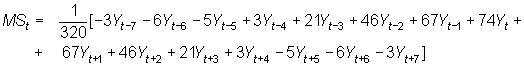
Puede verse que es una media móvil "ponderada", simétrica (los pesos a ambos lados del valor central son iguales) y con pesos negativos para valores alejados del valor central.

Pulsa aquí para ver una ilustración de este método de extracción de la tendencia mediante medias móviles, en un modelo de composición aditiva.

En cuanto a la valoración de este método, posee la ventaja de no requerir un modelo previo (una forma funcional establecida) y la posibilidad de actuar sobre el orden de la media, lo que permite extraer componentes más bien tendenciales o más bien ciclo-tendenciales. Sus inconvenientes, paradójicamente van por el mismo lado, ya que no existe criterio para elegir el orden (salvo la práctica habitual de hacerlo coincidir con la estacionalidad, m) y el hecho de que se pierden datos en los dos extremos de la serie (si p es par, se pierden p/2 al comienzo de la serie, y otros tantos al final, mientras que si es impar, la pérdida es de (p-1)/2 a cada lado)