Conceptos fundamentales
La inferencia estadística se desarrolla en
tres niveles complementarios:
-
Estimación puntual. Su objetivo es dar a una característica poblacional
desconocida un valor "razonable'', normalmente el valor que toma para una muestra
concreta un estadístico,
reflejo muestral de la característica poblacional: la media muestral
para estimar la media poblacional, el coeficiente de correlación muestral
para estimar el coeficiente de correlación poblacional, etc.
-
Intervalo de confianza. Su objetivo
es obtener un intervalo de posibles valores de la característica
poblacional en el que confiamos, en cierta medida, que se encuentre su
verdadero valor, esto es, un intervalo que
cubra al verdadero valor con una determinada probabilidad/confianza.
-
Contraste de hipótesis. Enunciada
una hipótesis
sobre una característica poblacional (y su contraria), su objetivo
es, en principio, aceptar (no rechazar) la hipótesis más
acorde con los datos.
La inferencia estadística presenta
dos enfoques
-
Inferencia
paramétrica.
Suponemos que los datos siguen una cierta distribución tipo con
uno o más parámetros (características poblacionales)
desconocidos. El objetivo de la inferencia paramétrica es "decir
algo'' sobre el valor de dichos parámetros en base a la información
parcial sobre la población que proporciona una muestra.
-
Inferencia
no paramétrica.
Sin suposiciones previas sobre la distribución de los datos (acaso ciertas
suposiciones de simetría o continuidad), se establece una hipótesis
sobre el comportamiento aleatorio de los mismos (sobre su mediana, aleatoriedad,
distribución, independencia, igualdad de distribución, etc.)
y, mediante un contraste de hipótesis se acepta (no se rechaza)
dicha hipótesis si no es incompatible con los datos.
A continuación desarrollaremos el procedimiento de los contrastes de
hipótesis paramétricos si bien los primeros conceptos e intuiciones
son válidos también para los no paramétricos.
Establecidas dos hipótesis
sobre el valor de un parámetro,
se construye una regla de decisión sobre dichas
hipótesis a partir de los datos muestrales. Así, se plantea
una hipótesis (y su alternativa) sobre una característica
de la población. Un contraste es una regla
de decisión
sobre dicha hipótesis (se acepta / no se rechaza o se rechaza
/ no se acepta) a partir de la información incompleta que proporciona
una muestra. Los contrastes también se denominan test o pruebas
estadísticas. Si la población
sigue una cierta distribución, las hipótesis se concretan
en valores de los parámetros: contrastes de hipótesis paramétricas;
en caso contrario, contrastes de hipótesis no paramétricas. |
Supongamos que tratamos de tomar una decisión
sobre la probabilidad de cara, p, en una moneda, utilizando
la información que proporcionan
20 lanzamientos. Planteamos como hipótesis a contrastar el que la ''moneda
es normal'', hipótesis que se puede concretar en términos del parámetro
de una distribución
de Bernouilli,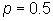 
;
se trata, por tanto, de un contraste de hipótesis paramétricas.
Las
hipótesis pueden ser simples o compuestas según incluyan
una especificación única ()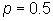
o múltiple (
)
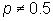de la característica
poblacional.
La hipótesis nul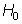a, 
,
es la hipótesis a contrastar. Habitualmente incluye una especificación única
de la característica poblacional. Es la hipótesis ''normal'',
la que nos queremos creer, y sólo rechazaremos si existen evidencias
significativas en su contra.
La hipótesis alternativa,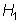 
,
es la hipótesis complementaria. Puede incluir una especificación única
de la característica
poblacional (contrastes de hipótesis simples sin interés
práctico) o múltiples especificaciones (contrastes de hipótesis
compuesta). Según incluyan especificaciones a los ''dos lados'' o sólo
a ''un lado'' de la
especificación de la hipótesis nula ()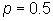
hablaremos de contrastes bilaterales o contrastes unilaterales. En el ejemplo,
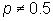(moneda
cargada), se trata de un contraste bilateral; si fuese es 
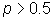(moneda
cargada hacia caras), sería unilateral.
El estadístico de la prueba permite
obtener la probabilidad de que ocurra la muestra obtenida bajo la hipótesis
nula (a veces también bajo la alternativa); en el ejemplo, S, "número
de caras obtenidas". Da una
medida de la discrepancia entre lo esperado bajo 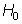(en el ejemplo, mitad de caras y mitad de cruces) y lo observado (el número
de caras, s, obtenido), discrepancia medida
en términos de probabilidad.
La región crítica o
de rechazo,
R.C., es el conjunto de valores muestrales para los cuales se rechaza .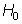
Su complementario es la región de aceptación, R.A.,
conjunto de valores muestrales para los cuales se acepta .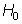
Determinada una de ellas queda
determinada la regla de decisión, el contraste. Su determinación
se realiza con el criterio de equivocarse lo menos posible. En el ejemplo,
donde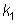 
y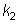 
son los valores o puntos
críticos,
las fronteras entre la aceptación y el rechazo en términos del
estadístico.
Al tomar una decisión se pueden producir
dos tipos de errores:
- Error de tipo I, rechazar 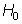siendo verdadera.
- Error de tipo II, aceptar 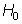siendo falsa.
Las probabilidades de ambos errores son:
-
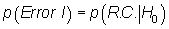, probabilidad que siempre se puede calcular.
,
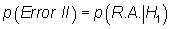probabilidad que en muchas situaciones no se pueden calcular.
Dado que ''apostamos'' por ,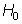
trataremos de encontrar una regla de decisión
(una región crítica) cuya probabilidad de error de tipo I no
supere un cierto umbral y que la probabilidad de error de tipo II, cumplida
la anterior
condición, sea mínima.
El límite máximo de la probabilidad de error de tipo I es el nivel
de significación,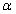 
,
habitualmente 0.10, 0.05 o 0.01. Fijado un nivel de significación, se
determinarán
los puntos críticos, con lo cual quedará
concretada la regla de decisión.
Un concepto que
simplifica la toma de decisión es el p-valor, definido
e interpretado en los siguientes términos:
- Probabilidad, bajo ,
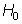de obtener una muestra tan o más "rara" que la obtenida.
- Riesgo, medido en términos de probabilidad,
de rechazar 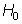siendo verdadera.
- Probabilidad de que la discrepancia entre lo observado y lo esperado sea
achacable al azar.
- Si p-valor>,
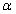se acepta ;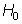
si p-valor<,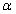
se rechaza .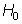
En la hoja adjunta se ilustran todos estos
conceptos.
