Algunos contrastes de hipótesis no paramétricas
Mediante procedimientos no paramétricos se pueden resolver contrastes de muy diversa naturaleza.
Así, los contrastes de bondad de ajuste permiten contrastar la distribución de probabilidad de una variable categórica o numérica.
Por otro lado, cuando no se puede aceptar
que los datos de una variable numérica siguen una cierta distribución
tipo, habitualmente la distribución normal, el problema de contrastar
la media de la población, ![]() ,
se transforma en contrastar la mediana, Me, valor de la variable que
divide a
la población en dos partes iguales, la mitad de los individuos presenta
valores de la variable menores o iguales que la mediana y la otra mitad presenta
valores superiores a la mediana. Los contrastes de mediana permiten
contrastar si los datos son compatibles con una cierta mediana teórica
,
se transforma en contrastar la mediana, Me, valor de la variable que
divide a
la población en dos partes iguales, la mitad de los individuos presenta
valores de la variable menores o iguales que la mediana y la otra mitad presenta
valores superiores a la mediana. Los contrastes de mediana permiten
contrastar si los datos son compatibles con una cierta mediana teórica ![]() .
.
Cuando se dispone de una variable cuantitativa X en
las dos poblaciones (subpoblaciones), determinadas por las modalidades de una
característica cualitativa dicotómica, el objetivo fundamental
es comparar su distribución; esto es,
estudiar si la variable cuantitativa (variable respuesta) presenta diferencias
significativas en cada uno de los dos niveles de la variable cualitativa (factor).
Denotaremos por ![]() y
y ![]() a
la variable cuantitativa en cada una de las dos situaciones. Si las variables,
por su peculiaridad (rangos, calificaciones, etc.) o por rechazarse la hipótesis,
no pueden considerarse con distribución normal (u otra distribución
tipo), se tratará de contrastar si
a
la variable cuantitativa en cada una de las dos situaciones. Si las variables,
por su peculiaridad (rangos, calificaciones, etc.) o por rechazarse la hipótesis,
no pueden considerarse con distribución normal (u otra distribución
tipo), se tratará de contrastar si ![]() y
y ![]() siguen
la misma distribución (contrastes de igualdad de distribución).
siguen
la misma distribución (contrastes de igualdad de distribución).
Para poder realizar estas comparaciones se utilizan dos muestras provenientes de individuos diferentes (estudiar las posibles diferencias salariales en función del sexo a partir de una muestra de hombres y una muestra de mujeres); en este caso hablaremos de muestras independientes. A veces se puede utilizar una muestra con los mismos individuos para las dos situaciones de la variable (comparar la valoración de dos detergentes a partir de los datos que sobre uno y otro proporciona una única muestra de consumidores); en este caso hablaremos de muestras apareadas o relacionadas. Siempre que se puedan considerar muestras relacionadas, este procedimiento proporciona en principio mejores inferencias.
Los problemas de inferencia sobre dos variables en una población tratan de ver si existe relación entre las mismas a partir de la información muestral. Si las dos variables son categóricas se trata de ver si son independientes y, en caso contrario, cuál es la intensidad de la dependencia o asociación (contrastes de independencia).
| Bondad de ajuste | C. de la |
|
| C. de Kolmogorov-Smirnov | ||
| Mediana | C. de signos | |
| C. de rangos con signo de Wilcoxon | ||
| Comparación de dos poblaciones | Muestras independientes | C. de Kolmogorov-Smirnov |
| C. de rachas de Wald-Wolfowitz | ||
| C. de la U de Mann-Whitney | ||
| Muestras relacionadas | C. de signos | |
| C. de rangos con signo de Wilcoxon | ||
| Independencia | C. de la |
|
1. Contrastes de bondad de ajuste
1.1. Contraste de bondad
de ajuste de la ![]() de Pearson
de Pearson
Sean ![]() las k modalidades
exhaustivas y mutuamente excluyentes de la característica A;
se dispone de n observaciones de A, siendo
las k modalidades
exhaustivas y mutuamente excluyentes de la característica A;
se dispone de n observaciones de A, siendo ![]() las
correspondientes a la modalidad
las
correspondientes a la modalidad ![]() . Se
trata de contrastar la distribución de probabilidad de esta característica:
. Se
trata de contrastar la distribución de probabilidad de esta característica:
A partir del estadístico ![]() de
Pearson y su distribución aproximada bajo
de
Pearson y su distribución aproximada bajo ![]() ,
,
se rechaza esta hipótesis cuando
siendo ![]() el
valor que en una distribución
el
valor que en una distribución ![]() deja
a su derecha una probabilidad de
deja
a su derecha una probabilidad de ![]() .
.
El estadístico mide la discrepancia
entre la frecuencia observada o empírica, ![]() ,
y
la frecuencia
esperada o teórica bajo
,
y
la frecuencia
esperada o teórica bajo ![]() ,
, ![]() :
discrepancias significativamente grandes llevan a rechazar
:
discrepancias significativamente grandes llevan a rechazar ![]() .
.
Además,
donde ![]() es
el valor muestral del estadístico.
es
el valor muestral del estadístico.
En la hoja adjunta se muestra un ejemplo de este contraste.
Si la determinación de las
probabilidades ![]() exige
la estimación
de s parámetros, la distribución del estadístico
bajo
exige
la estimación
de s parámetros, la distribución del estadístico
bajo ![]() resulta
una
resulta
una ![]() .
.
En principio, esta prueba permite contrastar la distribución de sucesos no numéricos (por ejemplo, opinión empresarial sobre la situación de su cartera de pedidos en los próximos meses, “peor”, “igual” o “mejor”). Para contrastar si unos datos numéricos (tamaño familiar, renta,...) se ajustan a una distribución hay que agrupar sus valores en intervalos, en especial cuando la distribución a contrastar es continua. En la hoja adjunta se muestra un ejemplo del contraste en esta situación.
1.2. Contraste de bondad de ajuste de Kolmogorov-Smirnov
Se trata de contrastar si unos datos numéricos se ajustan a una distribución teórica, esto es, si una variable X sigue una cierta distribución:
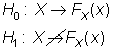 |
Para ello se compara la función de
distribución empírica,
![]() , con la función
de distribución teórica,
, con la función
de distribución teórica, ![]() ,
mediante el
estadístico de Kolmogorov-Smirnov,
,
mediante el
estadístico de Kolmogorov-Smirnov, ![]() ,
que mide la discrepancia entre
las mismas,
,
que mide la discrepancia entre
las mismas,
La distribución de dicho estadístico
bajo ![]() es
conocida en ciertas situaciones, por ejemplo cuando se contrasta la normalidad
(distribución
de Lilliefors). De manera general, cuando n es grande,
se
utiliza
el estadístico
es
conocida en ciertas situaciones, por ejemplo cuando se contrasta la normalidad
(distribución
de Lilliefors). De manera general, cuando n es grande,
se
utiliza
el estadístico
![]() , cuya distribución
aproximada bajo
, cuya distribución
aproximada bajo ![]() es
conocida
(distribución de Kolmogorov-Smirnov).
es
conocida
(distribución de Kolmogorov-Smirnov).
Se rechaza ![]() si existen discrepancias significativamente
grandes entre la función
de distribución empírica y la función de distribución
teórica; esto es, si
si existen discrepancias significativamente
grandes entre la función
de distribución empírica y la función de distribución
teórica; esto es, si
donde ![]() y
y ![]() son
los valores que en la distribución de Lilliefors
y en la de Kolmogorov-Smirnov, respectivamente, dejan a la derecha
una probabilidad de
son
los valores que en la distribución de Lilliefors
y en la de Kolmogorov-Smirnov, respectivamente, dejan a la derecha
una probabilidad de ![]() .
.
Además,
donde ![]() y
y
![]() hacen referencia
a la distribución de Lilliefors, para muestras de tamaño n, y
de Kolmogorov-Smirnov,
respectivamente, y
hacen referencia
a la distribución de Lilliefors, para muestras de tamaño n, y
de Kolmogorov-Smirnov,
respectivamente, y ![]() es
el valor muestral del
estadístico.
es
el valor muestral del
estadístico.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
2. Contrastes no paramétricos sobre una variable numérica
2.1. Contraste de los signos
Sea una variable X, disponiéndose
de una muestra de tamaño n, ![]() .
Se trata de contrastar si la mediana Me toma un determinado valor
.
Se trata de contrastar si la mediana Me toma un determinado valor ![]() :
:
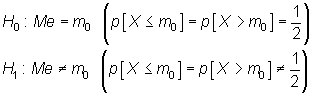 |
Para ello se considera p, la proporción
de valores de X menores 0 iguales que la mediana de la prueba ![]() .
Entonces
el contraste de mediana se reformula como un contraste de proporciones:
.
Entonces
el contraste de mediana se reformula como un contraste de proporciones:
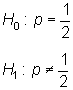 |
A partir del estadístico, S, número
de valores muestrales menores que la mediana ![]() ,
y su distribución bajo
,
y su distribución bajo ![]()
donde n* es el número de observaciones distintas
de ![]() ,
se rechaza esta hipótesis cuando
,
se rechaza esta hipótesis cuando
siendo a y b los
valores que en la distribución ![]() dejan
en cada cola una probabilidad no superior a
dejan
en cada cola una probabilidad no superior a ![]() .
Esto es, se rechaza
.
Esto es, se rechaza ![]() cuando
hay discrepancias significativamente grandes entre el número de valores
muestrales menores que la mediana de la prueba
cuando
hay discrepancias significativamente grandes entre el número de valores
muestrales menores que la mediana de la prueba ![]() , S,
y el número
esperado bajo
, S,
y el número
esperado bajo ![]() ,
, ![]() .
.
Además,
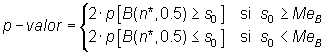 |
donde ![]() es
el valor muestral del estadístico y
es
el valor muestral del estadístico y ![]() la
mediana de la correspondiente distribución binomial.
la
mediana de la correspondiente distribución binomial.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
2.2. Contraste de los rangos con signo de Wilcoxon
Sea una variable X, disponiéndose
de una muestra de tamaño n, ![]() .
Se trata de contrastar si la mediana Me toma un determinado valor
.
Se trata de contrastar si la mediana Me toma un determinado valor ![]() :
:
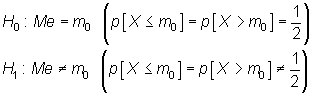 |
Para ello se calculan los rangos de las
diferencias absolutas de X respecto de ![]() ,
, ![]() ,
donde
,
donde ![]() , y
se consideran los estadísticos
, y
se consideran los estadísticos ![]() y
y ![]() ,
,
 |
cuya suma es la suma de los n primeros rangos,
Si ![]() es
la mediana poblacional, alrededor de la mitad de los valores de la muestra
estará por encima de
es
la mediana poblacional, alrededor de la mitad de los valores de la muestra
estará por encima de ![]() (diferencias
positivas) y el resto, por debajo (diferencias negativas); además, el
tamaño de las diferencias positivas
y de las negativas tendrá una distribución similar. Por tanto,
(diferencias
positivas) y el resto, por debajo (diferencias negativas); además, el
tamaño de las diferencias positivas
y de las negativas tendrá una distribución similar. Por tanto, ![]() y
y ![]() serán
parecidos.
serán
parecidos.
A partir del estadístico de Wilcoxon,
cuya distribución bajo ![]() es
conocida, se rechaza esta hipótesis
cuando
es
conocida, se rechaza esta hipótesis
cuando
siendo k el valor
que en la correspondiente distribución deja a su izquierda una probabilidad
de ![]() . Esto
es, se rechaza
. Esto
es, se rechaza ![]() cuando W toma valores
significativamente pequeños, cuando
cuando W toma valores
significativamente pequeños, cuando ![]() y
y ![]() toman
valores significativamente distintos.
toman
valores significativamente distintos.
Además,
donde ![]() es
el valor muestral del estadístico.
es
el valor muestral del estadístico.
El test de los signos desprecia parte de la información de la muestra (utiliza si el valor es mayor o menor que la mediana teórica, pero no el tamaño de esta discrepancia). El test de los rangos con signo permite utilizar tanto el signo de la diferencia entre el valor de X y la mediana teórica como el valor de dicha diferencia.
El contraste admite planteamiento unilateral, razonándose
en este caso con uno de los dos estadísticos, ![]() u
u ![]() .
.
En la hoja adjunta se muestra un ejemplo de este contraste.
3. Contrastes no paramétricos sobre una variable numérica en dos poblaciones
Contraste de igualdad de distribución: Muestras independientes
3.1. Contraste de Kolmogorov-Smirnov
Sean las variables ![]() y
y ![]() ,
disponiéndose de sendas muestras aleatorias de tamaño
,
disponiéndose de sendas muestras aleatorias de tamaño ![]() y
y ![]() .
Se trata de contrastar si
.
Se trata de contrastar si ![]() y
y ![]() siguen
la misma distribución:
siguen
la misma distribución:
 |
Para ello se comparan las dos funciones de distribución
empíricas, ![]() y
y ![]() ,
mediante el estadístico de Kolmogorov-Smirnov,
que mide la discrepancia entre
las mismas,
,
mediante el estadístico de Kolmogorov-Smirnov,
que mide la discrepancia entre
las mismas,
La distribución de dicho estadístico
bajo ![]() es conocida
en ciertas situaciones, por ejemplo cuando
es conocida
en ciertas situaciones, por ejemplo cuando ![]() .
De manera general, cuando
.
De manera general, cuando ![]() y
y ![]() son
grandes, se utiliza el estadístico
son
grandes, se utiliza el estadístico 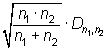 ,
cuya distribución aproximada bajo
,
cuya distribución aproximada bajo ![]() es
conocida (distribución de Kolmogorov-Smirnov).
es
conocida (distribución de Kolmogorov-Smirnov).
Se rechaza ![]() si
existen discrepancias significativamente grandes entre las funciones de
distribución empírica; esto es, si
si
existen discrepancias significativamente grandes entre las funciones de
distribución empírica; esto es, si
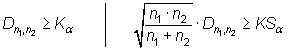 |
donde ![]() y
y ![]() son
los valores que en las correspondientes distribuciones dejan a la derecha
una probabilidad de
son
los valores que en las correspondientes distribuciones dejan a la derecha
una probabilidad de ![]() .
.
Además,
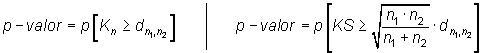 |
donde ![]() y
y
![]() hacen referencia
a la distribución
del estadístico cuando
hacen referencia
a la distribución
del estadístico cuando ![]() y
a la distribución de Kolmogorov-Smirnov, respectivamente, y
y
a la distribución de Kolmogorov-Smirnov, respectivamente, y ![]() es
el valor muestral del estadístico.
es
el valor muestral del estadístico.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
Contraste de igualdad de distribución: Muestras independientes
3.2. Contraste de rachas de Wald-Wolfowitz
Sean las variables ![]() y
y ![]() ,
disponiéndose de sendas muestras aleatorias de tamaño
,
disponiéndose de sendas muestras aleatorias de tamaño ![]() y
y ![]() .
Se trata de contrastar si
.
Se trata de contrastar si ![]() y
y ![]() siguen
la misma distribución:
siguen
la misma distribución:
 |
Para ello se ordenan conjuntamente las dos muestras. Si tienen la misma distribución, cabe esperar que los valores de una y otra muestra estén muy mezclados, es decir, que haya muchas rachas (secuencia de valores de una misma muestra).
A partir del
estadístico R, número de rachas, cuya distribución
bajo ![]() es conocida,
se rechaza esta hipótesis cuando
es conocida,
se rechaza esta hipótesis cuando
siendo k el valor
que en la correspondiente distribución deja a su izquierda una probabilidad
de ![]() . Esto
es, se rechaza
. Esto
es, se rechaza ![]() cuando R toma valores
significativamente pequeños, cuando los valores de las muestras están
poco mezclados.
cuando R toma valores
significativamente pequeños, cuando los valores de las muestras están
poco mezclados.
Además,
donde ![]() es
el valor muestral del estadístico.
es
el valor muestral del estadístico.
Si existen muchos empates entre las dos muestras, este contraste no es recomendable.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
Contraste de igualdad de distribución: Muestras independientes
3.3. Contraste de la U de Mann-Whitney
Sean las variables ![]() y
y ![]() ,
disponiéndose de sendas muestras aleatorias de tamaño
,
disponiéndose de sendas muestras aleatorias de tamaño ![]() y
y ![]() .
Se trata de contrastar si
.
Se trata de contrastar si ![]() y
y ![]() siguen
la misma distribución:
siguen
la misma distribución:
 |
Para ello se ordenan conjuntamente las muestras y se asigna
a cada valor su rango. Se consideran los estadísticos ![]() y
y ![]() ,
,
cuya suma es la suma de los n primeros rangos,
y los estadísticos ![]() y
y ![]() ,
,
cuya suma es
Además,
A partir del estadístico W de Wilcoxon o del estadístico U de Mann-Whitney,
cuyas distribuciones bajo ![]() son
conocidas, se rechaza esta hipótesis cuando
son
conocidas, se rechaza esta hipótesis cuando
siendo k el valor
que en la correspondiente distribución deja a su izquierda una probabilidad
de ![]() . Esto
es, se rechaza
. Esto
es, se rechaza ![]() cuando W y
U toman valores
significativamente pequeños, cuando
cuando W y
U toman valores
significativamente pequeños, cuando ![]() y
y ![]() 0
0 ![]() y
y ![]() toman
valores significativamente distintos.
toman
valores significativamente distintos.
Además,
donde ![]() y
y
![]() son el
correspondiente valor muestral del estadístico.
son el
correspondiente valor muestral del estadístico.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
Contraste de igualdad de distribución: Muestras relacionadas
3.4. Contraste de los signos
Sean las variables ![]() y
y ![]() ,
disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Se trata de contrastar
si
,
disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Se trata de contrastar
si ![]() y
y ![]() siguen
la misma distribución:
siguen
la misma distribución:
 |
A partir del estadístico S,
número
de diferencias positivas entre los valores de
las variables para cada individuo, y su distribución
bajo ![]() ,
,
donde n* es el número de diferencias no nulas, se rechaza esta hipótesis cuando
siendo a y b los
valores que en la distribución ![]() dejan
en cada cola una probabilidad no superior a
dejan
en cada cola una probabilidad no superior a ![]() .
Esto es, se rechaza
.
Esto es, se rechaza ![]() cuando
hay discrepancias significativamente grandes entre el número de
diferencias positivas observado o empírico, S,
y el número esperado bajo
cuando
hay discrepancias significativamente grandes entre el número de
diferencias positivas observado o empírico, S,
y el número esperado bajo ![]() ,
,
![]() .
.
Además,
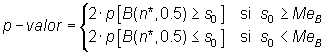 |
donde ![]() es
el valor muestral del estadístico y
es
el valor muestral del estadístico y ![]() la
mediana de la correspondiente distribución binomial.
la
mediana de la correspondiente distribución binomial.
El contraste admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de este contraste.
Contraste de igualdad de distribución: Muestras relacionadas
3.5. Contraste de los rangos con signo de Wilcoxon
Sean las variables ![]() y
y ![]() ,
disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Se trata de contrastar
si
,
disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Se trata de contrastar
si ![]() y
y ![]() siguen
la misma distribución:
siguen
la misma distribución:
 |
Para ello se calculan los rangos de las diferencias
absolutas entre ![]() y
y ![]() y
se consideran los estadísticos
y
se consideran los estadísticos ![]() y
y ![]() ,
,
 |
cuya suma es la suma de los n primeros rangos,
Si ![]() y
y ![]() tienen
la misma distribución, alrededor de la mitad de los valores
de la muestra de
tienen
la misma distribución, alrededor de la mitad de los valores
de la muestra de ![]() será
mayor que el correspondiente valor de
será
mayor que el correspondiente valor de ![]() (diferencias
positivas) y el resto, menor (diferencias negativas); además,
el tamaño de las diferencias positivas y de las negativas tendrá una
distribución similar. Por tanto,
(diferencias
positivas) y el resto, menor (diferencias negativas); además,
el tamaño de las diferencias positivas y de las negativas tendrá una
distribución similar. Por tanto, ![]() y
y ![]() serán
parecidos.
serán
parecidos.
A partir del estadístico de Wilcoxon,
cuya distribución bajo ![]() es
conocida, se rechaza esta hipótesis cuando
es
conocida, se rechaza esta hipótesis cuando
siendo k el
valor que en la correspondiente distribución deja
a su izquierda una probabilidad
de ![]() . Esto es, se rechaza
. Esto es, se rechaza ![]() cuando
W toma valores significativamente pequeños, cuando
cuando
W toma valores significativamente pequeños, cuando ![]() y
y ![]() toman
valores significativamente distintos.
toman
valores significativamente distintos.
Además,
donde ![]() es
el valor muestral del estadístico.
es
el valor muestral del estadístico.
El test de los signos desprecia parte de
la información de la muestra (utiliza si el valor de ![]() es
mayor o menor que el de
es
mayor o menor que el de![]() ,
pero no el tamaño de esta
discrepancia). El test de los rangos con signo permite utilizar tanto el signo
de la diferencia
entre el valor de
,
pero no el tamaño de esta
discrepancia). El test de los rangos con signo permite utilizar tanto el signo
de la diferencia
entre el valor de ![]() y de
y de ![]() ,
como el valor de dicha diferencia.
,
como el valor de dicha diferencia.
El contraste admite planteamiento unilateral,
razonándose en este caso con uno de los dos estadísticos, ![]() u
u ![]() .
.
En la hoja adjunta se muestra un ejemplo de este contraste.
4. Contraste de independencia entre variables categóricas
4.1. Contraste de independencia de
la ![]() de Pearson
de Pearson
Sean ![]() las k modalidades
exhaustivas y mutuamente excluyentes de la característica A y
las k modalidades
exhaustivas y mutuamente excluyentes de la característica A y ![]() las p modalidades
exhaustivas y mutuamente excluyentes de la característica B;
se dispone de n observaciones conjuntas de A y B,
siendo
las p modalidades
exhaustivas y mutuamente excluyentes de la característica B;
se dispone de n observaciones conjuntas de A y B,
siendo ![]() (frecuencia
absoluta conjunta) el número de observaciones del par de modalidades
(frecuencia
absoluta conjunta) el número de observaciones del par de modalidades ![]() .
Se
trata de contrastar la independencia entre ambas características:
.
Se
trata de contrastar la independencia entre ambas características:
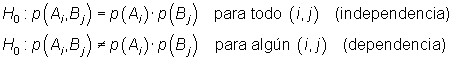 |
Para ello se comparan las frecuencias
observadas o empíricas, ![]() ,
con las frecuencias esperadas o teóricas bajo la hipótesis de
independencia,
,
con las frecuencias esperadas o teóricas bajo la hipótesis de
independencia, ![]() ,
siendo
,
siendo ![]() y
y ![]() (frecuencias
absolutas marginales) el número
de observaciones de la modalidad
(frecuencias
absolutas marginales) el número
de observaciones de la modalidad ![]() de
A y de
de
A y de ![]() de
B, respectivamente.
de
B, respectivamente.
A partir del estadístico ![]() de
Pearson y su distribución aproximada bajo
de
Pearson y su distribución aproximada bajo ![]() ,
,
|
se rechaza esta hipótesis cuando
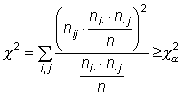 |
siendo![]() el
valor que una distribución
el
valor que una distribución ![]() deja
a su derecha una probabilidad
de
deja
a su derecha una probabilidad
de ![]() .
.
Además,
donde ![]() es el
valor muestral del estadístico.
es el
valor muestral del estadístico.
Dependiendo de las características de cada una de las variables (nominales u ordinales) existen otros estadísticos (Tau, d de Sommer, Gamma,...) con interpretación probabilística.
En la hoja adjunta se muestra un ejemplo de este contraste.