Intervalos de confianza en poblaciones normales
Una población
Si la variable a analizar es numérica, el objetivo principal de la inferencia por intervalos de confianza es alguna medida de posición (media o mediana), de dispersión (varianza) o algún otro parámetro poblacional. Así, si se cuenta con información muestral sobre el número de horas diarias que un individuo está viendo la televisión, trataremos de estimar, puntualmente y por intervalo, el promedio de horas en la población.
En
principio, si hacemos inferencia sobre un resumen de la variable
podemos considerar que dicha variable sigue una distribución y plantear
el problema desde la óptica paramétrica. Esa distribución
puede ser cualquiera de las muchas distribuciones tipo (binomial, Poisson,
normal, uniforme, gamma,...). Ahora bien, por distintos motivos (variables,
originales o transformadas, con distribución más o menos
campaniforme, teorema del límite central, simplicidad en los procedimientos,
...), lo más
habitual es la suposición de normalidad. Entonces, suponiendo que la variable X sigue
una
distribución normal de media ![]() y
desviación
y
desviación ![]() ,
estimaremos mediante intervalos de confianza
,
estimaremos mediante intervalos de confianza ![]() y
y ![]() .
.
Dos poblaciones
En este caso, el objetivo fundamental es
comparar la distribución
de una variable cuantitativa X en las dos poblaciones (subpoblaciones)
determinadas por las modalidades de una característica cualitativa dicotómica
o, lo que es lo mismo, estudiar si la variable cuantitativa (variable respuesta)
presenta diferencias significativas en cada uno de los dos niveles de la variable
cualitativa (factor). Esta comparación se realizará a partir
de la información parcial que proporcionan dos muestras. Denotaremos
por ![]() y
y ![]() a
la variable cuantitativa en cada una de las dos situaciones.
a
la variable cuantitativa en cada una de las dos situaciones.
Si podemos aceptar normalidad, el objetivo general de comparar dos poblaciones se traduce en comparar las medias de la variable en cada una de ellas; aunque suele tener únicamente un interés instrumental, también se pueden comparar las varianzas.
Para poder realizar estas comparaciones se utilizan dos muestras provenientes de individuos diferentes (estudiar las posibles diferencias salariales en función del sexo a partir de una muestra de hombres y una muestra de mujeres); en este caso hablaremos de muestras independientes. A veces se puede utilizar una muestra con los mismos individuos para las dos situaciones de la variable (comparar la valoración de dos detergentes a partir de los datos que sobre uno y otro proporciona una única muestra de consumidores); en este caso hablaremos de muestras apareadas o relacionadas. Siempre que se puedan considerar muestras relacionadas, este procedimiento proporciona en principio mejores inferencias.
| Poblaciones normales | Una población | I. de C. sobre la media | |
| I. de C. sobre la varianza | |||
| Dos poblaciones | Muestras independientes | I. de C. sobre la diferencia de medias | |
| I. de C. sobre el cociente de varianzas | |||
| Muestras relacionadas | I. de C. sobre la diferencia de medias | ||
Intervalo de confianza sobre la media poblacional
Sea X una
variable con distribución
normal de media ![]() y
desviación
y
desviación ![]() y
una muestra de tamaño n,
y
una muestra de tamaño n, ![]() .
.
A partir del estadístico
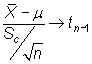 |
se construye el siguiente intervalo:
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
Véase en la hoja adjunta un ejemplo de este intervalo.
A partir del estadístico
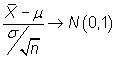 |
se puede construir el intervalo
siendo ![]() el
valor que en una distribución normal estándar deja a
su derecha una probabilidad de
el
valor que en una distribución normal estándar deja a
su derecha una probabilidad de ![]() .
Para ello se requiere del conocimiento de
.
Para ello se requiere del conocimiento de ![]() ,
algo en principio poco realista. A veces se utiliza cuando n es
grande para variables normales, estimando previamente
,
algo en principio poco realista. A veces se utiliza cuando n es
grande para variables normales, estimando previamente ![]() ,
o para variables no normales, en base al teorema del límite central.
,
o para variables no normales, en base al teorema del límite central.
Intervalo de confianza sobre la varianza poblacional
Sea X una variable con distribución
normal de media ![]() y
desviación
y
desviación ![]() y
una muestra de tamaño n,
y
una muestra de tamaño n, ![]() .
.
A partir del estadístico
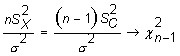 |
se construye
el intervalo
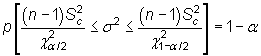 |
siendo ![]() y
y ![]() los
valores que en una distribución
los
valores que en una distribución
![]() con n-1
grados de libertad
dejan a su derecha una probabilidad de
con n-1
grados de libertad
dejan a su derecha una probabilidad de ![]() y
y
![]() ,
respectivamente.
,
respectivamente.
Véase en la hoja adjunta un ejemplo de este intervalo.
Intervalo de confianza sobre la diferencia de medias poblacionales
Sean ![]() y
y ![]() variables
normales, de media
variables
normales, de media ![]() y
y ![]() y
de varianza
y
de varianza ![]() y
y ![]() ,
respectivamente,
e independientes, disponiéndose de
sendas
muestras
aleatorias
de tamaño
,
respectivamente,
e independientes, disponiéndose de
sendas
muestras
aleatorias
de tamaño ![]() y
y ![]() :
:
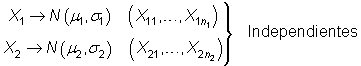 |
El estadístico
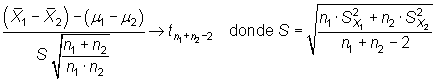 |
si las varianzas se pueden suponer iguales, y el estadístico
 |
en caso contrario, permiten construir los siguientes intervalos:
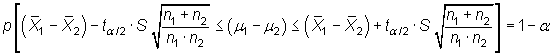 |
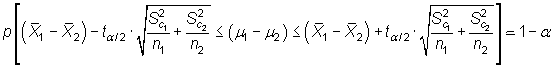 |
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
Véase en la hoja adjunta un ejemplo de intervalo sobre la diferencia de medias.
Intervalo de confianza sobre el cociente de varianzas poblacionales
Sean ![]() y
y ![]() variables
normales, de media
variables
normales, de media ![]() y
y ![]() y
de varianza
y
de varianza ![]() y
y ![]() ,
respectivamente, e independientes, disponiéndose de sendas muestras
aleatorias de tamaño
,
respectivamente, e independientes, disponiéndose de sendas muestras
aleatorias de tamaño ![]() y
y ![]() :
:
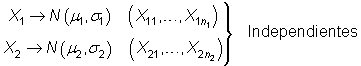 |
El estadístico
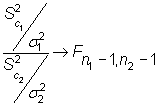 |
permite construir el intervalo de confianza
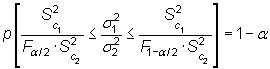 |
siendo ![]() y
y
![]() los valores
que en una distribución F con
los valores
que en una distribución F con ![]() y
y ![]() grados
de libertad dejan a su derecha una probabilidad de
grados
de libertad dejan a su derecha una probabilidad de ![]() y
y![]() , respectivamente.
, respectivamente.
Véase en la hoja adjunta un ejemplo de intervalo sobre el cociente de varianzas.
Intervalo de confianza sobre la diferencia de medias poblacionales
Sean ![]() y
y ![]() variables,
de media
variables,
de media ![]() y
y ![]() ,
respectivamente, disponiéndose de sendas muestras
aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Entonces se puede
considerar la variable
,
respectivamente, disponiéndose de sendas muestras
aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Entonces se puede
considerar la variable ![]() ,
de la que se dispone de una muestra aleatoria simple,
,
de la que se dispone de una muestra aleatoria simple, ![]() ,
donde
,
donde ![]() , variable
que se supone normal de media
, variable
que se supone normal de media ![]() y
de varianza
y
de varianza ![]() :
:
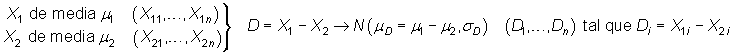 |
El estadístico
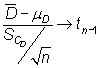 |
permite construir el intervalo de confianza
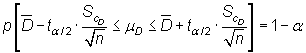 |
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
Véase en la hoja adjunta un ejemplo de este intervalo.