Ejercicios

Ejercicio 1. Sean y dos estimadores insesgados de varianza y , respectivamente, siendo ambos independientes entre sí. Buscar el valor de , para que es insesgado y tiene la menor varianza.

Ejercicio 2. Sea una variable de Poisson, e Y una variable con función de densidad

¿Cumplen las condiciones de regularidad de Crámér-Rao?

Ejercicio 3. Sea una muestra aleatoria simple de una población con función de densidad

a) Obtener el estimador máximo verosímil de .

b) Comprueba que

c) Estudia las propiedades del estimador obtenido

Ejercicio 4. Sea X una variable aleatoria con distribución geométrica de parámetro .

a) Demostrar que, para una muestra aleatoria simple de tamaño n, el estimador máximo verosímil de y su estimador por el método de los momentos, coinciden.

b) Estudiar si dicho estimador () es insesgado, suficiente, eficiente y consistente.

c) Calcular y el estimador máximo verosímil de dicha probabilidad.

Solución 1. Es insesgado para cualquier valor de . Por otro lado, la varianza alcanza su mínimo para , lo que se comprueba derivando. En definitiva, es el estimador de menor varianza entre los que son de esa forma.

Solución 2. Para la primera, , luego se cumplen. Para la segunda, , luego no se cumple la segunda condición.

Solución 3. a) El neperiano de la función de verosimilitud vale

de donde se comprueba que el E.M.V. es

b) Se comprueba haciendo directamente un cambio de variable

c)

Solución 4. a) 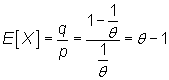, de donde , y será el estimador por el método de los momentos.

Por otro lado, , con lo que , y derivando

derivada que igualada a cero proporciona como estimador máximo verosímil.

b) Se comprueba que es insesgado, eficiente, suficiente y consistente.

c) Obsérvese que

sin más que tener en cuenta que la suma muestral es binomial negativa. Esa probabilidad es una función creciente (inyectiva) del estimador máximo verosímil, por lo que el estimador máximo verosímil de dicha probabilidad se obtendrá sustituyendo,