Ejemplo. Supongamos
una población de Bernoulli, ![]() ,
con
,
con ![]() . Podemos
imaginarnos esta población como una moneda cuya probabilidad de obtener
cara es p. Se supone que p es desconocida, y que tratamos
de estimarla.
. Podemos
imaginarnos esta población como una moneda cuya probabilidad de obtener
cara es p. Se supone que p es desconocida, y que tratamos
de estimarla.
Obtenemos una realización, ![]() ,
de una m.a.s.
,
de una m.a.s. ![]() o,
utilizando la imagen de la moneda, lanzamos cuatro veces la moneda de forma
independiente, representando las cuatro variables aleatorias,
o,
utilizando la imagen de la moneda, lanzamos cuatro veces la moneda de forma
independiente, representando las cuatro variables aleatorias, ![]() ,
cada una de las tiradas, y
,
cada una de las tiradas, y ![]() los
resultados de los lanzamientos. Por ejemplo, obtenemos (1,1,0,1), éxito
en las tiradas primera, segunda y cuarta, y fracaso en la tercera.
los
resultados de los lanzamientos. Por ejemplo, obtenemos (1,1,0,1), éxito
en las tiradas primera, segunda y cuarta, y fracaso en la tercera.
La función de probabilidad
de la población puede escribirse como ![]() ,
para x=0,1, de donde la función de probabilidad de la muestra
resulta
,
para x=0,1, de donde la función de probabilidad de la muestra
resulta
![]()
En concreto, para n=4,
![]()
Como hemos señalado, si la probabilidad de éxito, p, es conocida, esta función proporciona las probabilidades de las distintas realizaciones. Por ejemplo, si sabemos que p=0.3,
![]()
o
![]()
Pero si p es desconocida, obtenemos la función de verosimilitud. Como la realización de la muestra ha sido (1,1,0,1), dicha función será
![]()
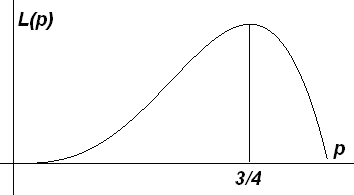 |
Por ejemplo, L(0.3)=0.0189 o L(0.5)=0.0625. La figura adjunta muestra esta función. Nótese, por ejemplo, que la verosimilitud de p=0.3 es el 30% de la verosimilitud de p=0.5, esto es, es mucho más verosímil p=0.5 que p=0.3.
Como antes dijimos, la verosimilitud es la probabilidad de que ocurra lo que efectivamente ha ocurrido. Muestra la diferente credibilidad que muestran los distintos valores del parámetro una vez obtenidos los datos muestrales.
La verosimilitud no es una probabilidad sobre p y sólo se utiliza en términos relativos, comparando las verosimilitudes para distintos valores de p, como en el párrafo anterior. Por ejemplo, el valor p=0.5 siempre tiene la misma verosimilitud, L(0.5)=0.0625, ocurra el resultado que ocurra. Ello no quiere decir que el hecho de que la moneda no esté cargada es igualmente razonable para cualquier realización de la muestra, porque para cada realización, habrá que comparar su verosimilitud con la de otros valores del parámetro.
¿Cómo aprovechar la información proporcionada por la función de verosimilitud en relación con la estimación de p? Una posibilidad consiste en fabricar un intervalo de valores creíbles de p. Algunos autores, por ejemplo, sugieren denominar "creíbles" o "viables" a los valores cuya verosimilitud relativa es superior a 0.1 (al 10%) ("increíbles" o "inviables" a los que no cumplan esta condición), "muy creíbles" o "muy viables" si es superior a 0.5 (al 50%) y "muy inviables" o "muy increíbles" si no supera 0.01 (el 1%). Las cifras son, por supuesto arbitrarias, aunque son bastante populares.
Por ejemplo, con esta terminología (y dado que hemos obtenido los resultados (1,1,0,1)), son muy inviables los valores de p inferiores a 0.106 o superiores a 0.998; son viables o creíbles los del intervalo (0.241 , 0.989) y son muy viables o muy creíbles los del intervalo (0.461 , 0.935).
Otra posibilidad es elegir como estimación de p el
valor más creíble (más verosímil), aquél
que tiene mayor verosimilitud (verosimilitud relativa igual a la unidad). Esa
estimación se denomina máximo-verosímil. En nuestro caso,
la estimación de p sería ![]() .
.