Métodos generales de estimación
La función de verosimilitud
En el recorrido anterior por la estimación paramétrica, se
disponía de una población, ![]() ;
para estimar el parámetro q, se obtenía
una realización,
;
para estimar el parámetro q, se obtenía
una realización, ![]() ,
de una muestra aleatoria simple,
,
de una muestra aleatoria simple, ![]() .
La estimación puede realizarse porque ambos elementos (realización y parámetro)
están relacionados. El elemento que los relaciona es la función de densidad
o de probabilidad de la muestra,
.
La estimación puede realizarse porque ambos elementos (realización y parámetro)
están relacionados. El elemento que los relaciona es la función de densidad
o de probabilidad de la muestra,
![]()
Esa aplicación es una función de n+1 variables, que juega dos papeles, esto es, puede verse de dos formas diferentes:
Resaltemos esta definición:
Sea
definida para |
Obsérvese que está definida sólo para los posibles valores
del parámetro, ![]() .
Además,
.
Además, ![]() tiene
que ser una realización posible de la muestra, y se supone conocida. De hecho,
a veces se escribe la función de verosimilitud como L(q) para indicar que es
sólo función del parámetro.
tiene
que ser una realización posible de la muestra, y se supone conocida. De hecho,
a veces se escribe la función de verosimilitud como L(q) para indicar que es
sólo función del parámetro.
La letra "L" que se emplea universalmente para designar la función de verosimilitud proviene del término inglés likelihood, verosimilitud.
Con frecuencia se utiliza la denominada "verosimilitud relativa", que cambia la escala de las verosimilitudes de forma que la función tome sus valores entre cero y uno. Fijemos la definición:
En las condiciones de la definición anterior, se denomina función de verosimilitud relativa a la función del parámetro
definida para |
Ilustremos estas definiciones con un ejemplo que, además de construir una función de verosimilitud, explota sus posibilidades de cara a la estimación de parámetros.
Ejemplo. Supongamos
una población de Bernoulli, Obtenemos una realización, La función
de probabilidad de la población puede escribirse como
En concreto, para n=4,
Como hemos señalado, si la probabilidad de éxito, p, es conocida, esta función proporciona las probabilidades de las distintas realizaciones. Por ejemplo, si sabemos que p=0.3,
o
Pero si p es desconocida, obtenemos la función de verosimilitud. Como la realización de la muestra ha sido (1,1,0,1), dicha función será
Por ejemplo, L(0.3)=0.0189 o L(0.5)=0.0625. La figura adjunta muestra esta función. Nótese, por ejemplo, que la verosimilitud de p=0.3 es el 30% de la verosimilitud de p=0.5, esto es, es mucho más verosímil p=0.5 que p=0.3. Como antes dijimos, la verosimilitud es la probabilidad de que ocurra lo que efectivamente ha ocurrido. Muestra la diferente credibilidad que muestran los distintos valores del parámetro una vez obtenidos los datos muestrales. La verosimilitud no es una probabilidad sobre p y sólo se utiliza en términos relativos, comparando las verosimilitudes para distintos valores de p, como en el párrafo anterior. Por ejemplo, el valor p=0.5 siempre tiene la misma verosimilitud, L(0.5)=0.0625, ocurra el resultado que ocurra. Ello no quiere decir que el hecho de que la moneda no esté cargada es igualmente razonable para cualquier realización de la muestra, porque para cada realización, habrá que comparar su verosimilitud con la de otros valores del parámetro. ¿Cómo aprovechar la información proporcionada por la función de verosimilitud en relación con la estimación de p? Una posibilidad consiste en fabricar un intervalo de valores creíbles de p. Algunos autores, por ejemplo, sugieren denominar "creíbles" o "viables" a los valores cuya verosimilitud relativa es superior a 0.1 (al 10%) ("increíbles" o "inviables" a los que no cumplan esta condición), "muy creíbles" o "muy viables" si es superior a 0.5 (al 50%) y "muy inviables" o "muy increíbles" si no supera 0.01 (el 1%). Las cifras son, por supuesto arbitrarias, aunque son bastante populares. Por ejemplo, con esta terminología (y dado que hemos obtenido los resultados (1,1,0,1)), son muy inviables los valores de p inferiores a 0.106 o superiores a 0.998; son viables o creíbles los del intervalo (0.241 , 0.989) y son muy viables o muy creíbles los del intervalo (0.461 , 0.935). Otra posibilidad es elegir como estimación de p el valor más creíble (más verosímil), aquél que tiene mayor verosimilitud
(verosimilitud
relativa igual a la unidad). Esa estimación se denomina máximo-verosímil.
En nuestro caso, la estimación de p sería |
Cuando la población es discreta, la función de verosimilitud es la probabilidad de que ocurra la realización que efectivamente ha ocurrido. Cuando la población es continua, la función de verosimilitud es una densidad y no una probabilidad. De hecho, la probabilidad de que ocurra una realización concreta de la muestra es siempre igual a cero, sea cual sea el valor del parámetro. Pero la densidad de la muestra para una realización representa la probabilidad alrededor de esa realización, por lo que básicamente los razonamientos anteriores, que han sido desarrollados para variables discretas, se mantienen aunque la población sea continua.
Método de máxima verosimilitud
Como el ejemplo anterior ilustra, una posibilidad prudente,
cuando se desea una estimación puntual de un parámetro, consiste en elegir
como estimación el valor del parámetro que maximiza la función de verosimilitud
(dicho valor del parámetro será una función de ![]() porque
la función de verosimilitud depende de la realización de la muestra). Si esta
maximización la obtenemos para una realización cualquiera, dispondremos de
la expresión del estimador, que se denomina máximo-verosímil. Formalicemos
el resultado.
porque
la función de verosimilitud depende de la realización de la muestra). Si esta
maximización la obtenemos para una realización cualquiera, dispondremos de
la expresión del estimador, que se denomina máximo-verosímil. Formalicemos
el resultado.
Sea
recibe el nombre de estimación máximo-verosímil de q. La función de la muestra |
Esta práctica es tan habitual que se utiliza una notación
específica para dicho logaritmo, que a veces se denomina log-verosimilitud.
Se escribe como ![]() o,
de forma más abreviada, como
o,
de forma más abreviada, como ![]() .
En concreto,
.
En concreto,
![]()
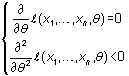
Con frecuencia, esta práctica proporciona el máximo o, al menos, indicaciones acerca de cómo obtenerlo. La primera de estas dos condiciones (anulación de la primera derivada) recibe el nombre de ecuación de verosimilitud.
Los siguientes ejemplos muestran cómo se desarrollan los cálculos analíticamente.
Ejemplo (continuación). Volvamos
sobre nuestra población de Bernoulli,
y su neperiano,
de donde la ecuación de verosimilitud resulta
cuya solución es Obviamente, si
la realización fue (1,1,0,1), la estimación resulta |
Ejemplo 1 (continuación). Para la estimación de la duración media de las bombillas, q = E[X], para una población de duraciones exponencial negativa, la función de verosimilitud es
cuyo neperiano resulta
cuya solución resulta |
Ejemplo 2 (continuación). En
el ejemplo 2, el recargo (porcentual)
era
donde, como puede observarse, las condiciones
las hemos escrito para q, ya que la función
debe verse como función de q.
Nótese, además que dichas condiciones equivalen a
Nótese que la derivada no se anula, sino que
es siempre negativa (la función es decreciente) por lo que el máximo
se encuentra en el primer valor en el que la función no se anula, esto
es, La gráfica muestra la función de verosimilitud y su máximo. |
La ilustración posterior muestra la dinámica de la máxima verosimilitud.
[Insertar un enlace a una hoja de cálculo]
Máxima verosimilitud para varios parámetros
El método de máxima verosimilitud se aplica de la misma manera si hay más de un parámetro a estimar, si bien con una mayor complejidad en el cálculo del máximo. La idea es totalmente similar:
Sea
recibe el nombre de estimación
máximo-verosímil de |
Ilustraremos el procedimiento con la estimación de los dos
parámetros, m y ![]() (nótese
que consideramos
(nótese
que consideramos ![]() ,
y no s como parámetro, por lo que las funciones
se escriben en función de
,
y no s como parámetro, por lo que las funciones
se escriben en función de ![]() y
con respecto al mismo se toman las derivadas) de
una población normal. La verosimilitud resulta
y
con respecto al mismo se toman las derivadas) de
una población normal. La verosimilitud resulta
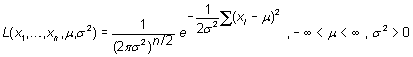
y su neperiano
![]()
La ecuación de verosimilitud es ahora un sistema de dos ecuaciones con dos incógnitas,
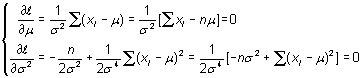
De la primera se obtiene ![]() ,
que sustituida en la segunda proporciona
,
que sustituida en la segunda proporciona ![]() ,
esto es,
,
esto es,![]() .
.
La matriz hessiana, sustituidos los parámetros por las soluciones de la ecuación de verosimilitud, resulta
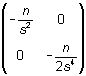
que claramente es definida negativa. En definitiva,
los estimadores máximo verosímiles son ![]() y
y ![]() .
.
Máxima verosimilitud e información parcial. Principio de máxima verosimilitud.
La idea que subyace al principio de la estimación máximo-verosímil (maximizar la probabilidad o la densidad de la realización de la muestra) se aplica también cuando no se conoce completamente la realización de la muestra, sino sólamente se dispone de información parcial sobre la misma. Esa información es un suceso, cuya probabilidad dependerá del parámetro; su maximización me proporcionará la estimación máximo verosímil. Resumimos esta idea en un enunciado:
Principio de máxima verosimilitud Sea
Si el suceso S incluye realizaciones concretas de una variable continua, se sustituirán adecuadamente las probabilidades por densidades. |
Un par de ejemplos aclararán el modo de trabajo con el principio de máxima verosimilitud:
Ejemplo. Se
quiere estimar la proporción de clientes de un hipermercado
que están
satisfechos del trato recibido. Para ello, se encuesta a 10 clientes
a la salida de la línea de cajas; entre ellos, 7 están
satisfechos, 2 no lo están y otro dice que se lo tiene que pensar.
Se trata, pues, de una población de Bernoulli, En este caso, la información es parcial, porque sabemos que hemos obtenido 7 éxitos (7 unos), 2 fracasos (2 ceros), pero el décimo resultado ignoramos si es éxito o fracaso (desconocemos también el orden de los resultados, pero esa información sabemos que no es información útil para estimar p). En definitiva, ha ocurrido un suceso S="7 u 8 éxitos en 10 tiradas independientes de Bernoulli de parámetro p" y, como el número de éxitos es una variable binomial, B(10,p), podemos escribir simbólicamente
con lo que
y la ecuación de verosimilitud resulta, tras operar un poco,
Las soluciones son, por un lado, p=0
y p=1 (que son mínimos; de hecho, para esos valores la probabilidad
vale cero) y por otro las soluciones de la ecuación de segundo grado.
Una de ellas es p=1.4866, que no consideramos por estar fuera
del intervalo [0,1], y la segunda p=0.7534. Se comprueba (la
comprobación no es difícil, pero sí pesada) que para este valor la segunda
derivada es negativa, con lo cual, para ese valor existe un máximo. En
definitiva, la estimación máximo verosímil de la proporción de clientes
satisfechos es Obsérvese que no se obtiene el mismo resultado
eliminando ese indeciso. En ese caso, tendríamos 7 éxitos y dos fracasos
en 9 tiradas de Bernoulli independientes, con lo que estimaríamos p como
la proporción muestral de éxitos, Algunos expertos en tratamiento de encuestas
sugieren desdoblar los indecisos en dos encuestados, uno a favor y otro
en contra. Los que están a favor se desdoblarían en dos, ambos a favor,
y los que están en contra en dos, ambos en contra. Nuestros 10 encuestados
se desdoblarían en 20, 15 a favor y 5 en contra. La estimación de p sería
ahora |
Ejemplo 1 (continuación). Para la estimación de la duración media de las bombillas, q = E[X], para una población de duraciones exponencial negativa, supongamos que sólo (¡sólo!)se dispone de 3 años para hacer la encuesta. Se ponen 5 bombillas en funcionamiento, una se funde en 0.8 años, otra en 1.2 años, una tercera en 2.2 años, y las otras dos no se funden en los 3 años disponibles, por lo que finaliza el experimento. Una posibilidad consiste en eliminar del estudio
las dos bombillas que no se han fundido, y estimar q por
máxima verosimilitud a partir de las tres restantes,
Se trata de maximizar su probabilidad pero, siendo continua la distribución de la población (exponencial negativa) las probabilidades de tres primeros sucesos deben sustituirse por la densidad. Así, hay que maximizar
que, teniendo en cuenta que
cuyo neperiano es
con solución |
Propiedades de los estimadores máximo-verosímiles
La popularidad del uso de los estimadores máximo-verosímiles
se basa en que es un buen estimador del parámetro. Enunciaremos, sin demostrar,
sus principales propiedades. En todas ellas supondremos que se dispone de una
población, ![]() ,
y que
,
y que![]() es una muestra
aleatoria simple de X
es una muestra
aleatoria simple de X
Invariancia Sea
|
Como puede verse, la propiedad de invariancia permite realizar la estimación máximo-verosímil en el terreno en que nos sea más cómodo. Veamos el siguiente ejemplo:
Ejemplo 1 (continuación). La
duración media de las bombillas, q =
E[X], se ha estimado por máxima verosimilitud como la duración
media de la muestra,
esto es, no es necesario escribir la verosimilitud como función de p para maximizarla, sino que puede utilizarse el estimador máximo-verosímil de q. |
Aunque ![]() sea
función de T, esto no quiere decir que
sea
función de T, esto no quiere decir que ![]() sea
suficiente, porque la función que los relaciona no tiene por qué ser biyectiva.
No obstante, habitualmente lo es, lo que implica que muchas veces el estimador
máximo verosímil es efectivamente un estimador suficiente.
sea
suficiente, porque la función que los relaciona no tiene por qué ser biyectiva.
No obstante, habitualmente lo es, lo que implica que muchas veces el estimador
máximo verosímil es efectivamente un estimador suficiente.
Eficiencia Supongamos que se cumplen las condiciones de regularidad de Cramér-Rao y que el estimador máximo verosímil se obtiene como solución de la ecuación de verosimilitud. Entonces, si existe un estimador eficiente, coincide con el estimador máximo verosímil. |
La anterior propiedad garantiza que, si hay un estimador eficiente (que de existir es único, como sabemos), el máximo verosímil es eficiente. Para ello se exige, claro está, que se cumplan las condiciones de regularidad de Cramér-Rao, porque de no ser así no podríamos hablar de estimadores eficientes; pero se exige también que el estimador máximo verosímil se obtenga por técnicas de derivación.
Comportamiento asintótico Supongamos que se cumplen las condiciones de regularidad de Cramér-Rao y que el estimador máximo verosímil se obtiene como solución de la ecuación de verosimilitud. Supongamos también que se cumplan ciertas condiciones de regularidad adicionales sobre la función de densidad o de probabilidad de la población (que no enunciaremos y que se cumplen en los casos de interés práctico). Entonces se cumple:
|
Obsérvese, en primer lugar, que las condiciones que se exigen son las mismas que las que garantizan la eficiencia del estimador, cuando existe. Además, se exigen ciertas condiciones de regularidad funcional que se cumplen en los casos que nosotros estudiamos, por lo que no las detallamos.
En cuanto a las conclusiones, obsérvese que, por la primera, se garantiza la consistencia del estimador.
Por la segunda, se obtiene la normalidad
como distribución aproximada del estimador máximo-verosímil, lo que permitirá
su uso para construir intervalos de confianza aproximados para q.
Pero, además, nótese que ![]() tiene
aproximadamente esperanza nula y varianza unidad, por lo que
tiene
aproximadamente esperanza nula y varianza unidad, por lo que
![]()
o, dicho de otra forma, la esperanza del estimador es aproximadamente igual al parámetro, y además,
![]()
o equivalentemente ![]() ,
esto es, la varianza del estimador es aproximadamente la cota de Cramér-Rao.
En definitiva, estos resultados se describen diciendo que, en las condiciones
del resultado anterior, el
estimador máximo verosímil es asintóticamente insesgado y asintóticamente eficiente.
,
esto es, la varianza del estimador es aproximadamente la cota de Cramér-Rao.
En definitiva, estos resultados se describen diciendo que, en las condiciones
del resultado anterior, el
estimador máximo verosímil es asintóticamente insesgado y asintóticamente eficiente.
Método de los momentos (de analogía)
El método de los momentos esta basado en una idea clásica que propone estimar las medias o varianzas poblacionales mediante las medias o varianzas muestrales, respectivamente. Por ello se denomina de analogía, porque su técnica consiste en sustituir las características poblacionales por las análogas muestrales.
El razonamiento básico que apoya este método es que si la muestra es representativa de la población, las características muestrales deberán ser representativas de las poblacionales.
La mayor ventaja de este método es su sencillez de aplicación, por lo que se sigue utilizando en situaciones en las que otros métodos se complican, o cuando el número de parámetros desconocidos a estimar es abundante.
No obstante, los estimadores obtenidos por este método no están muy cualificados.
Definamos el método y más adelante iremos viendo todas estas objeciones.
Sea
que puede resolverse con respecto a los parámetros,
Entonces, dada una muestra aleatoria
simple,
donde |
La elección de los k primeros momentos, y el hecho de que sean centrados respecto del origen (no centrales) es una simplificación. La idea es elegir aquellos momentos que simplifiquen más la resolución del sistema de ecuaciones y, por otro lado, que sean fáciles de calcular (del menor orden posible). Nótese también que las ecuaciones del sistema no son lineales, por lo que no está garantizado que el sistema tenga solución.
Ejemplo. Supongamos
que la población tiene una distribución
Conocemos la esperanza poblacional,
donde hemos escrito la media muestral, |
El siguiente ejemplo ilustra de manera sencilla la no univocidad de la solución.
Ejemplo. Supongamos
que la población tiene una distribución de Poisson,
|
Veamos otro ejemplo de aplicación.
Ejemplo. Un investigador desea estudiar la proporción p, de personas que defraudan a Hacienda en la declaración del IRPF. Temiendo que los encuestados contesten negativamente a una pregunta directa, utiliza el siguiente mecanismo: El encuestado lanzará al aire una moneda no cargada (sin que el encuestador vea el resultado). Si sale cara, responderá que sí es un defraudador, y si sale cruz responderá la verdad (sí o no, según su caso). Asociamos una variable, Y, a las respuestas
de los encuestados, con Y=1 si el encuestado responde afirmativamente,
y Y=0 si la respuesta es negativa. Los n encuestados vendrán
representados por la realización de una muestra aleatoria simple,
la esperanza de Y valdrá Obsérvese que si la media muestral de
respuestas positivas, |