El muestreo en poblaciones normales.

Si la muestra proviene de una población normal unidimensional entonces se tiene:

1. tiene una distribución . Demostración
2. tiene una distribución .
3. La media y la varianza muestral son independientes.

Si tenemos dos poblaciones, ambas normales, y nos interesa la diferencia poblacional, es evidente que el estadístico de interés sea la diferencia muestral.

Así, si la m.a.s.,, proviene de una y la muestra de una , admitiendo que ambas muestras son independientes entre sí., la primera de tamaño n y la segunda con m variables, se tiene que

es decir, que esta diferencia de dos muestras es una combinación lineal de m+n variables aleatorias normales independientes, siendo, por tanto, su distribución también normal, de media y varianza . Es decir,

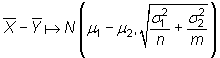Un caso particular importante se produce cuando ambas muestras las extraemos de la misma población. Así, se tendrá que las medias y las varianzas coinciden, es decir que y que , por tanto

Demostración:

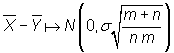Puesto que las n variables tienen la misma distribución y son independientes, entonces su suma es también normal .

Al dividir por n se tiene el resultado