Transformación de una variable aleatoria bidimensional

Sea (X,Y) una v.a. bidimensional con distribución conocida y sea (U,V) una transformación de ella del tipo U=g(X) y V=h(Y). Podemos estar interesados en obtener la distribución de (U,V).

• Si (X, Y) es discreta entonces (U,V) es también una v.a. bidimensional discreta y su función de probabilidad se obtiene a partir de la función de probabilidad de (X,Y) de la siguiente manera,

donde el sumatorio se extiende a los de (X,Y) tales que y .

• Si (X,Y) es continua, su transformada puede no ser variable aleatoria y puede no ser continua pero si se cumplen ciertas condiciones, (U,V) es variable bidimensional continua y su función de densidad conjunta se puede obtener aplicando el siguiente resultado (teorema del cambio de variable):

Proposición. Sea (X,Y) una v.a. bidimensional continua con función de densidad conjunta fXY. Sea u=g(x,y), v=h(x,y) una aplicación inyectiva de tal que existe, en su conjunto imagen, la transformación inversa y , y que sus derivadas parciales , , , son funciones continuas y además que el determinante jacobiano

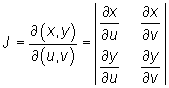
es distinto de cero.

Sea (U,V) la transformada de (X,Y) por (g,h), es decir, U=g(X,Y) y V=h(X,Y); entonces (U,V) es una variable aleatoria bidimensional continua y su función de densidad es

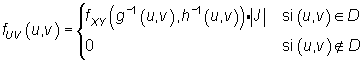donde .