CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS N-DIMENSIONALES

Vamos a estudiar las características de las variables aleatorias n-dimensionales al igual que hicimos en el caso de variables unidimensionales. Por simplicidad también en muchos casos nos vamos a referir al caso bidimensional (X,Y) aunque la generalización al caso n-variante es inmediata.

Así, si (X,Y) es una variable aleatoria bidimensional con función de distribución FXY y función de probabilidad (en el caso discreto) o función de densidad (en el caso continuo) fXY, podemos resumir ciertos aspectos de la distribución de probabilidad de esta variable a través de una serie de medidas teóricas características.

- La Esperanza de una función de (X,Y)

Sea (X,Y) una variable bidimensional y g una aplicación de tal que U= g(X,Y) es variable aleatoria unidimensional, llamamos esperanza de g(X,Y) al valor

• Si (X,Y) es discreta con valores

• Si (X,Y) es continua

   

  Ejemplo: Lanzándose dos dados perfectos, sea X el primer resultado e Y el segundo. Obtener el valor esperado de la variable suma de los dos resultados, es decir E(X+Y).

  E(X+Y)= (1+1) p[X=1,Y=1] + ... + (6+6) p[X=6,Y=6] = 7 puntos.

  O bien, podemos plantear

  E(X+Y) = E(X) + E(Y) = 3.5 + 3.5 = 7 puntos

Propiedades:

1. . En general,
2. , en general,
3. Sean X1, ..., Xn v.a. con la misma esperanza m, entonces, la esperanza de la v.a. media muestral es también m
4. La esperanza del producto de v.a. independientes es el producto de las esperanzas . En general,

    

- La Covarianza

La covarianza entre las variables X e Y es una medida que sirve para evaluar la relación lineal existente entre las dos variables.

Se define como

donde mX y mY son las esperanzas de X e Y respectivamente.

El valor de la covarianza entre X e Y se obtiene de acuerdo a las siguientes expresiones:

• Si (X,Y) es discreta con valores y fXY su función de probabilidad
• Si (X,Y) es continua y fXY su función de densidad

Propiedades:

	En general,
Si X e Y independientes, entonces:
	,
,
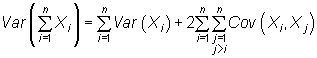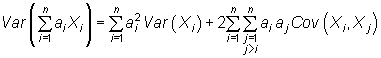Si X1, X2,.., Xn son variables independientes entonces
Si X1, X2,.., Xn son variables independientes con esperanza m y varianza , entonces
Sean y y sean , entonces
Sean y , entonces
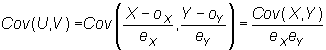Sean X1,..,Xn e Y1,..,Ym dos conjuntos disjuntos de variables aleatorias,
Sean X1,..,Xn un conjunto de variables aleatorias,

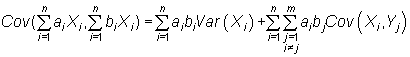- El Coeficiente de Correlación

El coeficiente de correlación lineal entre dos variables aleatorias X e Y se define como

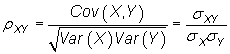Este coeficiente mide también como la covarianza la relación lineal entre dos variables, pero este coeficiente toma un valor en el intervalo [-1,1] lo que supone una ventaja a la hora de determinar el grado de relación entre las variables.

Cuando el coeficiente es cero se dice que las variables están incorrelacionadas. Si el coeficiente es positivo decimos que existe una correlación positiva entre ellas, es decir, que existe una relación lineal positiva entre ellas. Y si es negativo que la correlación es negativa, o bien, que existe una relación lineal negativa .

Propiedades:

1. 
2. Si X e Y son independientes entonces están incorrelacionadas (el recíproco no es cierto)
3. Sean y transformaciones lineales de X e Y con , entonces el coeficiente de correlación entre U y V es

   

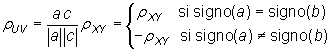
   Es decir, al coeficiente de correlación no le afectan los cambios de origen pero sí le pueden afectar los cambios de escala cambiando el tipo de relación entre las variables de positiva a negativa y al revés sin variar el grado de ésta.

4. Como caso particular de la propiedad anterior, si U y V son las variables X e Y tipificadas,y entonces la covarianza entre U y V es igual al coeficiente de correlación entre X e Y .

Ejemplo:

- La Esperanza condicionada

Dada (X,Y) variable aleatoria bidimensional se han estudiado las distribuciones condicionadas para una de las componentes dado el conocimiento que se tiene de la ocurrencia de la otra.

Pues bien, también se puede obtener la esperanza de esas distribuciones condicionadas y se denomina esperanza condicionada.

Así, si y es un valor posible de la variable Y, es decir, (con probabilidad estrictamente positiva si la variable es discreta o bien, un valor donde la densidad es distinta de cero si se trata de una v.a. continua). Entonces, llamamos esperanza de X condicionada por Y=y al valor, si existe,

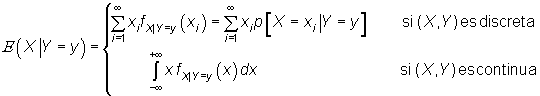También nos podemos plantear el cálculo de la esperanza de X condicionada a que para cualquier B suceso real e incluso condicionada a que ha ocurrido un suceso más general que compromete a ambas variables,, en estos casos se obtendría la esperanza condicionada para X como

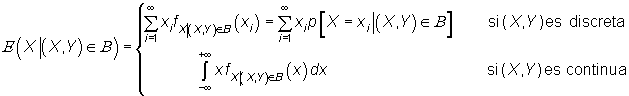Ejemplo

- La Varianza condicionada

También podemos calcular otros momentos condicionados como por ejemplo, la varianza condicionada.

Así si (X,Y) es una variable aleatoria bidimensional e y es un valor posible de la variable Y (con ) entonces definimos la varianza de X condicionada por Y=y como

Propiedades: