DISTRIBUCIONES n-DIMENSIONALES DISCRETAS

Multinomial:

La distribución multinomial es una generalización de la distribución binomial. En este caso, en un experimento interesa estudiar no la ocurrencia de un único suceso o la de su contrario, sino la de varios sucesos (tres o más).

La distribución multinomial, M(n,p1,...,pn) proporciona probabilidades de obtener, en m repeticiones independientes de un experimento, x1 veces el suceso A1, x2 veces el suceso A2,..., xn veces el suceso An, donde dichos sucesos forman una partición del espacio muestral, es decir, tal que para y donde , por tanto, se cumple .

Así, considerando que Xi es el número de veces que se presenta el suceso Ai en las m repeticiones tenemos que la variable n-dimensional (X1, X2, ..., Xn) sigue una distribución multinomial de parámetros n, p1, ..., pn y su función de probabilidad es

para con .

Hay que tener en cuenta que si (X1, X2, ..., Xn) es una variable multidimensional entonces existe una relación lineal entre sus componentes ya que X1+ X2+ ...+ Xn = m, por lo que, una de las variables, por ejemplo Xn, se puede poner como combinación lineal del resto, Xn=m-X1- X2- ...- Xn-1. Por tanto, el fenómeno que describe la variable (X1, X2, ..., Xn) queda igualmente descrito por una variable de una dimensión menor, (X1, X2, ..., Xn-1), sin que esta pérdida de dimensión suponga una pérdida de información.

Por ejemplo, una variable multinomial de dimensión dos (X1, X2), M(n,p1,p2), se puede describir considerando una cualquiera de sus componentes que tiene una distribución binomial, por lo que en realidad esta variable es unidimensional y no bidimensional.

Además, cada una de las n variables, Xi, que forman una multinomial M(n,p1,...,pn) siguen distribuciones binomiales B(m,pi), es decir, las distribuciones marginales de una multinomial son binomiales, por tanto, la esperanza y la varianza de cada una de estas variables es, E[Xi]=m·pi y Var(Xi)=mpi(1-pi). Además la covarianza entre dos cualesquiera de sus componentes es, .

Estos momentos de las variables componentes de una multinomial se pueden agrupar en forma de matriz dando lugar a las denominadas matriz de esperanzas y matriz de varianzas-covarianzas, que recogen las características teóricas principales de la distribución multinomial (medias, varianzas y covarianzas)

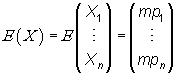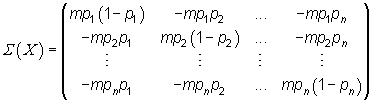Ejemplo: El entrenador de un equipo de baloncesto opina que los jugadores A, B y C tienen similares aptitudes para ser titulares del equipo en la posición de base. Así, determina que juegen el mismo número de minutos cada partido. Se sabe que el 40% de las canastas son de C, mientras que A y B consiguen un 30% de encestes. Calcular la probabilidad de que en un partido con 9 encestes de dos puntos, A consiguiera dos, B tres y C cuatro.

Sea la variable tridimensional que recoge el número de encestes de A, de B y de C, respectivamente. Dicha variable es una multinomial con n=9, p1=0.3, p2=0.3 y p3=0.4. Así,

Hipergeométrica Multivariante:

La distribución hipergeométrica multivariante H(N,m,p1,...,pn) es una generalización de la distribución hipergeómetrica. Proporciona probabilidades de extraer x1 bolas del color 1, x2 bolas del color 2,...y xn bolas del color n de una urna en la que hay N1,...Nn bolas de colores diferentes (N=N1+···+Nn). Realizamos m extracciones sin reposición , y consideramos las variables, Xi, número de bolas extraídas de color i (i = 1, 2, ..., n). La variable n-dimensional (X1, X2, ..., Xn) sigue una distribución hipergeométrica multivariante de parámetros N, m, p1, ..., pn, donde , es decir, la proporción de bolas de color i-ésimo (i= 1, 2,..,n) en la primera extracción.

NOTA: Si las extracciones se hiciesen con reposición entonces se trataría de una distribución multinomial.

La función de probabilidad de la distribución hipergeométrica multivariante es

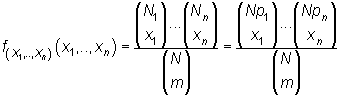para con y (i = 1, 2,..., n).

Además, igual que en la distribución anterior, hay que tener en cuenta que existe una relación lineal entre las variables componentes, X1+ X2+ ...+ Xn = m, por lo que, una de las variables, por ejemplo Xn, se puede poner como combinación lineal del resto, Xn=m-X1- X2- ...- Xn-1. Por tanto, el fenómeno que describe la variable (X1, X2, ..., Xn) queda igualmente descrito por una variable de una dimensión menor, (X1, X2, ..., Xn-1), sin que esta pérdida de dimensión suponga una pérdida de información.

Análogamente, una variable hipergeométrica multivariante de dimensión dos (X1, X2), H(N,m,p1,p2), se puede describir considerando una cualquiera de sus componentes que tiene una distribución hipergeométrica, por lo que en realidad esta variable es unidimensional y no bidimensional.

Además, cada una de las n variables, Xi, que forman una hipergeométrica H(N,m,p1,...,pn) siguen distribuciones hipergeométricas univariantes H(N,m,pi), es decir, las distribuciones marginales de una hipergeométrica multivariante son hipergeométricas, por tanto, la esperanza y la varianza de cada una de estas variables es, E[Xi]=m·pi y Var(Xi)=mpi(1-pi)(N-m)/(N-1). Además la covarianza entre dos cualesquiera de sus componentes es,

.

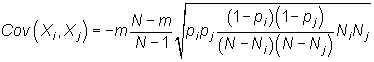Estos momentos de las variables componentes de una hipergeométrica multivariante se pueden agrupar en forma de matriz dando lugar a las denominadas matriz de esperanzas y matriz de varianzas-covarianzas, que recogen las características teóricas principales de la distribución hipergeométrica multivariante (medias, varianzas y covarianzas)

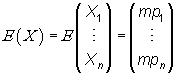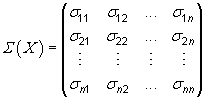donde

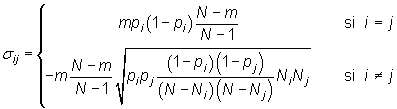
Ejemplo: En un equipo de baloncesto con 12 jugadores, han hecho una comisión de 4 representantes. En la plantilla hay 3 pivotes, 3 base y 6 aleros. ¿Cuál es la probabilidad de que haya 2 bases y 2 pivotes?

Tenemos una variable tridimensional que recoge el número de pivotes, bases y aleros, respectivamente, que forman parte de la comisión. Dicha variable es una hipergeométrica multivariante con N=12, n=4, N1=3, N2=3 y N3=6. Así,