DISTRIBUCIONES TIPO N-DIMENSIONALES CONTINUAS
Normal n-dimensional
La distribución normal n-dimensional Nn(m,S) es una generalización de la distribución normal univariante.
La función de densidad de una variable n-dimensional normal X=(X1, X2, ..., Xn) de parámetros m y S es
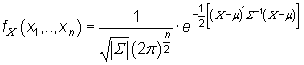 |
para ![]() (i = 1,2,..,n), donde m
es el vector de medias
(i = 1,2,..,n), donde m
es el vector de medias 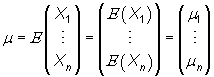 con
con ![]()
y S es la matriz
de varianzas-covarianzas (simétrica y definida positiva) 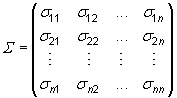 con y
con y ![]() .
.
Propiedades:
sigue una distribución normal n-dimensional Nn(m,S) donde S = A A'.
Z=BX+C |
tiene una distribución normal p-dimensional Np(Bm+C, BSB').
En particular con k=1, tenemos que la distribución marginal de cualquiera
de las Xi es una distribución normal unidimensional
![]() .
.
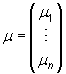 y
y 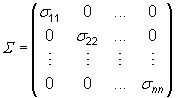 .
.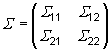 entonces
la distribución de
entonces
la distribución de
Esta distribución es un caso particular de la distribución normal n-dimensional para n=2 por lo que todos los resultados vistos anteriormente son también válidos.
No obstante, mostraremos de forma explícita dichos resultados sin recurrir a la notación matricial.
Así bien, la función de densidad de una variable aleatoria (X,Y) normal bidimensional es
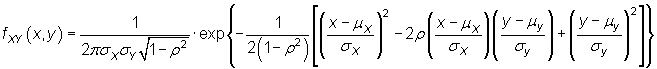 |
para ![]() y
y ![]() , donde mX
y mY son las medias de
X e Y respectivamente, sX
y sY sus desviaciones
típicas y r el coeficiente de correlación
lineal entre las dos variables.
, donde mX
y mY son las medias de
X e Y respectivamente, sX
y sY sus desviaciones
típicas y r el coeficiente de correlación
lineal entre las dos variables.
Propiedades:
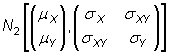 y
(U,V) es una transformación de ella del tipo
U=aX+bY+c
y V=dX+eY+f
, de manera que la matriz
y
(U,V) es una transformación de ella del tipo
U=aX+bY+c
y V=dX+eY+f
, de manera que la matriz Entonces la variable aleatoria (U,V) también sigue una distribución
normal bidimensional 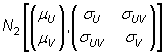 ,
donde
,
donde
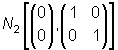 y
(U,V) es una transformación de ella del tipo anterior (con rg(B)=2)
entonces (U,V) sigue una distribución normal bidimensional
y
(U,V) es una transformación de ella del tipo anterior (con rg(B)=2)
entonces (U,V) sigue una distribución normal bidimensional
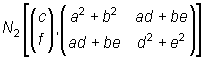
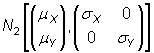 .
.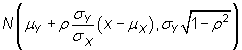 .
.