CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS UNIDIMENSIONALES

Sea X una variable aleatoria y sea su función de distribución y su función de probabilidad (si es discreta) o su función de densidad (si es continua).

Para resumir ciertos aspectos de la distribución de probabilidad de esta variable (definida a través de la distribución o de la densidad) se definen una serie de medidas teóricas características.

Dichas medidas se clasifican según cuál sea el tipo de resumen que se pretende obtener en:

Así, caracterizaremos la distribución de probabilidad de la variable aleatoria mediante resúmenes centrales (medidas de posición), medidas que nos proporcionan una idea del grado de concentración o dispersión de los valores de la variable alrededor de un valor central (medidas de dispersión) y mediante otras medidas que nos informan del perfil y la forma que tiene su función de probabilidad (si la variable es discreta) o bien su función de densidad (si la variable es continua).

MEDIDAS DE POSICIÓN

Las medidas de posición más habituales son: la esperanza, la mediana y la moda. Otras medidas que también se utilizan son los cuantiles.

- La Esperanza Matemática

La esperanza matemática o media teórica de una distribución es el principal resumen de una variable aleatoria.

Bajo ciertas condiciones (dispersión pequeña) esta medida es un buen resumen de la distribución de probabilidad.

Si X es una v.a. discreta que toma los valores y es su función de probabilidad entonces su esperanza se define a partir de la siguiente suma

Si X es una v.a. continua y es su función de densidad entonces se define su esperanza a partir de la siguiente integral:

 

Ejemplo 18 Cálculo esperanza discreta y continua

 

Además, podemos calcular directamente la esperanza de cualquier función de una variable aleatoria. Así bien, si X es una v.a. y g(X) es una v.a. función de X, la esperanza de g(X) se obtiene como

 

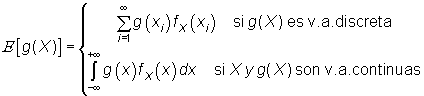Ejemplo 19 Cálculo esperanza función de una v.a.

Propiedades de la esperanza:

  1. Si X está acotada, , entonces su esperanza existe y .
  2. Si entonces
  3. Si X es una v.a. no negativa, , y su esperanza existe entonces también será no negativa
  4. La esperanza de una constante es la propia constante, .
  5. Sean g(X) y h(X) dos funciones v.a. de X existiendo sus respectivas esperanzas entonces
    En particular:
  6. Sean g(X) y h(X) dos funciones v.a. de X existiendo sus respectivas esperanzas tales que entonces
  7. Si existe la esperanza de X entonces
  8. Si la función de probabilidad o densidad de X es simétrica respecto de un valor a, su esperanza, si existe es dicho valor a.
  9. Sea Y la v.a. obtenida al aplicar un cambio de origen y de escala a la v.a. X, .Si la esperanza de X existe entonces la de Y también y se verifica que .

- La Mediana y cuantiles

La mediana es otra medida de posición central que proporciona aquél valor que deja la mitad de la probabilidad a la izquierda y la mitad a la derecha.

En general, si X es una v.a. la mediana es cualquier valor que verifica

y

En particular, si X es continua las anteriores condiciones se simplifican y la mediana es cualquier valor que verifica

 

De la misma forma, se definen otras medidas de posición denominados cuantiles. Así, el cuantil de orden q es cualquier valor que verifica:

y

es decir, cualquier valor que deja a la izquierda una probabilidad (al menos) q y el resto a su derecha. Análogamente, si X es continua el cuantil de orden q , es cualquier valor que verifica .

La mediana en realidad es el cuantil de orden q=0.5.

Ejemplo 20 cálculo mediana

 

- La Moda

Es otra medida de posición central que se define como el valor (o valores) de la variable en el que la función de probabilidad (en el caso discreto) o la de densidad (en el caso continuo) alcanza el máximo absoluto.

Ejemplo 21 moda

 

Las tres medidas de centralización vistas guardan la siguiente relación

 

MEDIDAS DE DISPERSIÓN

Las medidas de dispersión indican el grado de concentración de los valores de la variable alrededor de una medida de posición central, dando, a su vez, una idea de la representatividad de esta medida de centralización como resumen global de la variable.

Las medidas de dispersión más utilizadas son: la varianza, la desviación típica y el coeficiente de variación.

- La Varianza

La varianza es una medida absoluta de la dispersión de los valores de una variable respecto de su media.

Sirve por un lado, para valorar el grado de dispersión de los valores de una distribución, permitiendo la comparación con otras distribuciones, y por otro, proporciona una medida de la representatividad de la esperanza como resumen global de la distribución.

Sea X una variable aletoria cuya esperanza es . Se llama varianza de X al número

Si X es una v.a. discreta que toma los valores y es su función de probabilidad entonces su varianza se obtiene como

Si X es una v.a. continua y es su función de densidad entonces su varianza vale

 

Ejemplo 22 Cálculo varianza

Propiedades de la varianza:

  2. La varianza de una variable es cero si, y solo si, es una v.a. degenerada, es decir, es constante
  3. y se alcanza la igualdad cuando
  5. Sea Y la v.a. obtenida al aplicar un cambio de origen y de escala a la v.a. X, . La varianza de la variable transformada es (sólo afectan los cambios de escala no de origen)

- La Desviación Típica o Desviación Estándar

La desviación típica es también una medida absoluta de la dispersión que se define a partir de la varianza como

Frente a la varianza esta nueva medida presenta la ventaja de estar dada en las mismas unidades de la variable.

Propiedades de la desvieción típica:

  1. La desviación típica es cero si, y solo si, la variable es constante
  3. Sea Y la v.a. obtenida al aplicar un cambio de origen y de escala a la v.a. X, . La desviación típica de la variable transformada es (sólo afectan los cambios de escala no de origen)

- El Coeficiente de Variación

El coeficiente de variación es una medida relativa de la dispersión de la distribución de una variable definido como

Este coeficiente mide la dispersión respecto del tamaño de la variable, tamaño medido en términos de su esperanza.

Además, aunque no le afectan los cambios de escala sí se ve afectado por los cambios de origen. En concreto, si Y es la v.a. obtenida al aplicar un cambio de origen y de escala a la v.a. X, , el coeficiente de variación de Y es

Ejemplo 23

 

MEDIDAS DE FORMA

La finalidad de estas medidas está en conocer si las probabilidades se distribuyen simétricamente alrededor de la media y si dicha distribución tiene un comportamiento similar a la distribución de probabilidad más importante: la 'distribución Normal'(enlace)

Las medidas de forma utilizadas son: el coeficiente de asimetría y el coeficiente de curtosis.

- El Coeficiente de Asimetría

Este coeficiente, adimensional e invariante frente a cambios de origen y escala, vale cero cuando la variable es simétrica y está definido como

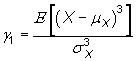Para distribuciones unimodales con desviación a la derecha (figura1) el coeficiente es positivo y se dice que la distribución es asimétrica positiva o a la izquierda. Por el contrario, para distribuciones unimodales con desviación a la izquierda (figura 2) el coeficiente toma un valor negativo y se dice que la distribución es asimétrica negativa o a la derecha.

FIGURA 1 FIGURA 2

 

- El Coeficiente de Curtosis o Apuntamiento

Para estudiar el aplastamiento o apuntamiento de las distribuciones continuas unimodales se utiliza el coeficiente de curtosis definido como

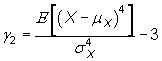Este coeficiente, también adimensional e invariante ante cambios de origen y de escala, toma el valor cero cuando la distribución presenta el mismo perfil que la distribución normal correspondiente (de misma media y varianza).

Si la distribución es más apuntada que la normal entonces el coeficiente es positivo y se dice que la distribución es leptocúrtica; si es más aplastada el coeficiente es negativo y se dice que la distribución es platicúrtica y si presenta el mismo perfil que la normal entonces es cero y se denomina distribución mesocúrtica.

FIGURA 3

En las distribuciones discretas no tiene sentido comparar el perfil de la función de probabilidad con el de la función de densidad normal, aún así, se puede obtener el coeficiente e interpretarlo en el sentido del reparto de la probabilidad en la recta real. Así, por ejemplo, en este caso un coeficiente positivo indica que la variable acumula más probabilidad en el centro y menos en las colas que la normal correspondiente, y si es negativo, justo al contrario.

 

EJERCICIOS FINALES

Ejemplo 24. Dada una distribución calcular todo: esperanza, mediana, moda, varianza, desviación típica, coeficiente de variación, coeficientes de asimetría y curtosis (vale el 6.16)

EJERCICIOS DE AUTOEVALUACIÓN

Proponer algún ejercicio como el anterior. ¿Incluir resultados?

 

Incluir el Tma. de Markov y la Desigualdad de Chebyshev?????????