Dependencia e independencia de sucesos

En algunas ocasiones aparecen dependencias entre dos sucesos, es decir, la ocurrencia (el hecho de que se verifique uno de ellos) influye en la ocurrencia del otro. Observa el siguiente ejemplo. En una baraja española suprimimos una carta, por ejemplo, el as de oros. A continuación, extraemos una carta elegida al azar. Obtenemos un premio si la carta extraída es un "Rey", suceso que denotamos por "R".

Utilizando la Regla de Laplace obtenemos: .

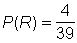Ahora, alguien nos informa que la carta extraída ha sido un oro, "O", ¿crees que esta información modificaría nuestra probabilidad de obtener premio?

Es inmediato que si el resultado ha sido un oro nuestras posibilidades son nueve, y el espacio muestral está formado por estas nueve cartas:

y tienes un único caso a tu favor (el rey de oros), con lo que obtendrás premio una de cada nueve veces, es decir 1/9=4/36, mejorando bastante nuestras posibilidades de éxito.

Observa que esto indica que, con una baraja como la del ejemplo, hay una cierta dependencia entre los sucesos "Rey" y "Oro", en estos casos se dice que ambos sucesos son dependientes. De hecho,

Sin embargo, si te planteas de nuevo el problema anterior cuando disponemos de una baraja completa, obtendrás que los sucesos "Rey" y "Oro" son independientes, ya que;

Concretando, dos sucesos A y B son independientes si la ocurrencia de uno no influye en la del otro o al revés y se verifica que

Si tienes en cuenta la definición de probabilidad condicionada, verás que dos sucesos son independientes, si cumplen una cualquiera de las tres condiciones siguientes: