Distribución de una variable aleatoria
Igual que en el caso unidimensional, una variable aleatoria bidimensional (X,Y) se caracteriza por su distribución, es decir, por el reparto de las probabilidades entre todos los valores (x,y) que tome.
Esta distribución se representa mediante dos funciones que asignan (de diferente forma) probabilidad a los valores que toma la variable:
Función de distribución
Se define la función de distribución (F.D.) de una variable (X,Y) en un punto (x,y) como:
Esta función en el punto del plano (x,y) acumula toda
la probabilidad asignada a todos los valores de la variable que se encuentran
en el rectánguno ![]() .
El esquema descrito
en la hoja de cálculo ilustra el comportamiento de una función
de distribución
de una variable bidimensional, (X,Y) . Asimismo, muestra los distintos valores
de la distribución en distintos puntos.
.
El esquema descrito
en la hoja de cálculo ilustra el comportamiento de una función
de distribución
de una variable bidimensional, (X,Y) . Asimismo, muestra los distintos valores
de la distribución en distintos puntos.
Propiedades de la función de distribución:
Al igual que en el caso unidimensional, si (X,Y) es una variable bidimensional discreta su función de distribución es escalonada con saltos en los puntos del plano correspondientes a los valores que toma la variable, sin embargo si (X,Y) es continua entonces su función de distribución es siempre continua.
Función de probabilidad
Si (X,Y) es una variable aleatoria bidimensional discreta se define su función de probabilidad (f.p.) en un punto (x,y) como:
Esta función en el punto (x,y) toma la probabilidad de que ocurra X=x e Y=y.
Es decir, si (X,Y) es una variable discreta que toma valores en
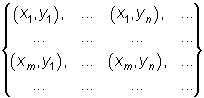
su función de probabilidad es ![]() para
para ![]() e igual
a cero para el resto de puntos del plano.
e igual
a cero para el resto de puntos del plano.
Propiedades de la función de probabilidad:
Las dos primeras propiedades caracterizan la f.p. de una v.a. discreta bidimensional.
Ejemplo: Se lanzan 2 dados perfectos y llamamos X=resultado del primer dado, Y=mínimo de los dos dados. Calculemos la función de probabilidad conjunta y sus marginales. En la hoja de cálculo se obtienen los resultados.
Además si conocemos la función de probabilidad podemos obtener la función de distribución y viceversa de la siguiente manera:
Función de densidad
Se dice que (X,Y) es una variable aleatoria bidimensional continua si:
Las variables bidimensionales continuas toman valores en todo el plano real o en un subconjunto (no numerable) del mismo.
Para este tipo de variables se define la función de densidad conjunta (f.d.) como
Propiedades de la función de densidad:
En particular, ![]()
![]()
Las dos primeras propiedades caracterizan la f.d. de una v.a. continua bidimensional.
Además si conocemos la función de densidad podemos obtener la función de distribución y viceversa de la siguiente manera:
Cálculo de probabilidades mediante la función de probabilidad
Si (X,Y) es una variable bidimensional discreta y fXY es su función de probabilidad podemos calcular la probabilidad de que (X,Y) tome valores en cualquier suceso B del plano de la siguiente manera
![]()
Cálculo de probabilidades mediante la función de densidad
Si (X,Y) es una variable bidimensional continua y fXY es su función de densidad podemos calcular la probabilidad de que (X,Y) tome valores en cualquier suceso B del plano de la siguiente manera
![]()
Distribuciones condicionadas
Si estamos interesados en el cálculo de probabilidades de sucesos referentes simultáneamente a ambas variables X e Y es necesario conocer la distribución conjunta (FXY o fXY). Sin embargo, el estudio del comportamiento probabilístico individual se hace a partir de las distribuciones marginales (FX, fX o FY, fY).
Pero puede suceder que conozcamos qué valor ha tomado una
de las dos variables, por ejemplo Y, y bajo esa información
queramos conocer la nueva distribución de la variable X.
El conocimiento del valor que toma una de las variables altera la distribución
de las probabilidades de la otra. En este caso, estamos hablando de obtener
la distribución de X condicionada
por el conocimiento de que Y ha tomado un valor concreto, ![]() y
y ![]() .
.
O bien, de forma más general, si conocemos que ![]() queramos
conocer la nueva distribución de X, es decir, su distribución
condicionada dada por
queramos
conocer la nueva distribución de X, es decir, su distribución
condicionada dada por ![]() o por
o por ![]() .
.
- Caso discreto
Sea (X,Y) una variable bidimensional discreta y sea fXY su función de probabilidad, vamos a calcular distintas distribuciones condicionadas para X :
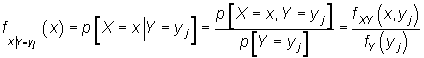
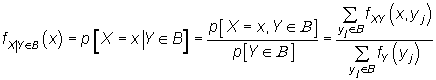
- Caso continuo
Sea (X,Y) una variable bidimensional continua y sea fXY su función de densidad, vamos a calcular distintas distribuciones condicionadas para X :
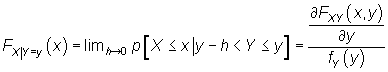
Expresión poco útil en la práctica, pero derivando respecto a x se obtiene la función de densidad condicionada de X como
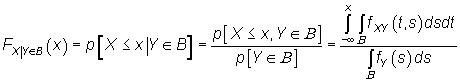
Y una vez hallada la F.D. derivando respecto a x se obtendría la f.d. condicionada.