.
Los valores de la magnitud para los distintos bienes en los distintos períodos
de
tiempo se recogen en la siguiente tabla:Frecuentemente, el interés no está en comparar precios, cantidades o valores de un único bien, sino en conocer la evolución conjunta de esas magnitudes para un grupo más o menos numeroso de bienes. Para ello, trataremos de resumir la información suministrada por los índices simples en un único índice que denominaremos compuesto, complejo o sintético. Nuestro propósito es obtener un número índice sencillo pero que reúna la mayor cantidad de información posible. Según que prime la sencillez o la conservación de la máxima información tendremos dos tipos de índices complejos: sin ponderar y ponderados.
Sea la magnitud X (precios, cantidades, valores,
...) relativa a k bienes, .
Los valores de la magnitud para los distintos bienes en los distintos períodos
de
tiempo se recogen en la siguiente tabla:
 |
A partir de los índices simples de X para cada uno de los bienes,
 |
podremos obtener un índice complejo para X utilizando un promedio, índice complejo que resume la información proporcionada por los índices simples. Los más habituales son los que se obtienen a partir de medias aritméticas o medias agregativas. También se pueden aplicar medias geométricas o medias armónicas.
Índices complejos sin ponderar. Todos los índices simples, y por tanto todas las componentes, tienen el mismo peso.
Media aritmética
 |
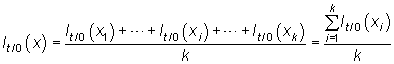Media agregativa
 |
El problema de la media agregativa es que exige que las componentes sean agregables.
Índices complejos ponderados.
En este caso, los índices simples tienen distinto peso, es decir, se
asignan diferentes ponderaciones a las componentes o magnitudes.
Sean estos pesos 
.
Media aritmética
 |
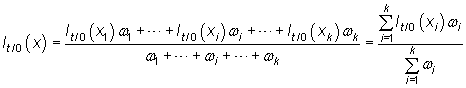Los índices complejos de media aritmética sin ponderar se pueden considerar un caso particular de éste, cuando todas las ponderaciones son iguales a 1.
Media agregativa
 |
Los índices complejos de media agregativa sin ponderar se pueden considerar un caso particular de éste, cuando todas las ponderaciones son iguales a 1. Además, las medias agregativas se pueden expresar como medias aritméticas ponderadas. Así, para la media agregativa sin ponderar resulta
 |
y para la media agregativa ponderada
 |
Por tanto, la media aritmética ponderada de los índices simples es la forma más general de agregar índices simples para obtener un índice complejo:
 |
donde 
son
las ponderaciones normalizadas,
 |
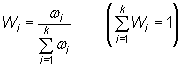Habitualmente estas ponderaciones se expresan en tanto por ciento o en tanto por mil.
Variación, repercusión y participación
El valor del índice en sí mismo, su nivel, aporta poca información: un índice que valga 167,3 indicaría que la magnitud ha experimentado un crecimiento del 67,3% desde el periodo base, periodo que pudiera estar muy alejado en el tiempo. La información más relevante es la variación del índice a corto plazo. Así, si el índice es de periodicidad mensual, la variación del índice se medirá mediante tres tipos de tasas:
Tasa de variación intermensual, esto es, la variación del índice un mes respecto del mes anterior:
 |
Suele ser una tasa muy volátil y compara dos periodos heterogéneos.
Tasa de variación en lo que va de año, es decir, la variación del índice un mes respecto del mes de diciembre del año anterior:
 |
De nuevo, compara periodos heterogéneos; su interés radica en que sirven de referencia para ciertos índices, como el Índice de Precios de Consumo, para los que se hacen predicciones sobre su crecimiento en el año.
Tasa de variación interanual, esto es, la variación del índice un mes respecto del mismo mes del año anterior:
 |
Dado que compara periodos homogéneos y recoge todo un año, es la tasa de variación más relevante para seguir la evolución de la magnitud.
No sólo va a interesar la variación (intermensual, en lo que va de año o interanual) de un índice, también interesará conocer qué parte de esa variación corresponde a cada una de las componentes o grupos de componentes que lo forman. La parte de la tasa de variación que es achacable a una componente o grupo de componentes se conoce como repercusión, resultando que la suma de las repercusiones de las distintas componentes es la tasa de variación. Las repercusiones se pueden expresar en porcentaje sobre la tasa de variación, lo que se denomina participación; en este caso, su suma es 100.
En el caso de un índice complejo, media aritmética ponderada de los índices simples con ponderaciones fijas, la repercusión del bien i-ésimo en la tasa de variación intermensual se calcula del siguiente modo:
 |
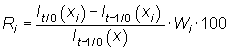pudiéndose demostrar que su suma es la correspondiente tasa de variación,
 |
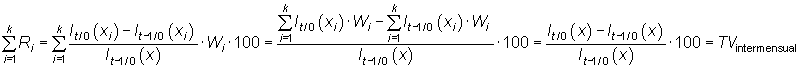En el mismo sentido se calcularían las repercusiones para los otros tipos de tasas. Como se puede observar, en la repercusión influye no sólo la variación de la componente, sino también su peso en el índice.
En la hoja adjunta se ilustran estos tres conceptos.