Tasas de variación
Como dijimos más arriba, el interés en el estudio de las series temporales reside habitualmente en la evaluación de sus cambios a lo largo del tiempo. Estos cambios se valoran a través de las denominadas tasas de variación, que surgen de la comparación de los valores de la serie en dos periodos de tiempo distintos.
Claro está que dependiendo de la componente de la serie que estudiemos, las variaciones serán más coyunturales, estacionales, o estructurales.
Variación absoluta
La variación absoluta de una serie temporal (también llamado incremento) es la diferencia entre dos valores de la serie. Por ejemplo, la variación absoluta de la magnitud con respecto al periodo anterior es
![]()
Cuando la serie temporal posee estacionalidad, a veces se calcula la variación en el periodo estacional. Veamos el siguiente ejemplo:
La tabla presenta el número de ocupados en la Construcción en Castilla y León durante los dos últimos años.
t |
2002:4 |
2003:1 |
2003:2 |
2003:3 |
2003:4 |
2004:1 |
2004:2 |
2004:3 |
117.3 |
115.4 |
118.4 |
116.4 |
113.7 |
116.9 |
119.3 |
118.8 |
En el tercer trimestre de 2004, hubo 118.8 miles de ocupados. Obsérvense las siguientes variaciones absolutas:
No obstante su sencillez, las variaciones absolutas no se utilizan separadas de otras medidas de variación, por la falta de referencias en su dimensión o escala. No es lo mismo que el crecimiento del número de ocupados sea de 2,400 en la Construcción de Castilla y León o en la Industria europea.
Las medidas absolutas de variación sólo sirven para evaluar su signo (positivo significa incremento, negativo significa incremento negativo o decremento) o para realizar comparaciones entre series del mismo orden de magnitud. Por ello se prefieren las variaciones denominadas relativas.
Variación relativa
Las variaciones relativas de una serie temporal, denominadas también tasas o tantos, son el cociente entre una variación absoluta y una medida del tamaño de la serie. A veces se multiplican por 100 para describirlas como porcentajes. La más conocida es la denominada "crecimientos básicos" de una serie temporal,

Obsérvese lo que indicábamos en el párrafo anterior, ya que los crecimientos básicos resultan de dividir el incremento de la serie entre el valor anterior de la misma, lo que da al incremento un marco de referencia.
La tabla siguiente muestra los crecimientos básicos de la serie de ocupados en la Construcción regional. Como puede verse, están descritos en porcentaje o tanto por ciento:
t
|
2003:1
|
2003:2
|
2003:3
|
2003:4
|
2004:1
|
2004:2
|
2004:3
|
-1.6%
|
2.6%
|
-1.7%
|
-2.3%
|
2.8%
|
2.1%
|
-0.4%
|
Por ejemplo, ![]()
La utilización de una medida de referencia en el denominador
crea el problema de su elección. Así, el valor elegido en los crecimientos
básicos (![]() )
hace que dicha tasa no sea simétrica. Por ejemplo, si tenemos una serie temporal
que toma los tres siguientes valores:
)
hace que dicha tasa no sea simétrica. Por ejemplo, si tenemos una serie temporal
que toma los tres siguientes valores:
 |
![]() ,
, ![]() ,
, ![]() ,
el crecimiento básico en el periodo 2 es del 20%,
,
el crecimiento básico en el periodo 2 es del 20%,
![]()
Sin embargo, el crecimiento básico en el periodo tercero no es del -20%,
![]()
sino del 16.7%, porque ahora la referencia es el valor 120, y no el valor 100, como antes. Se dice que los crecimientos básicos son "bondadosos", ya que premian los crecimientos, pero disminuyen la penalización de los decrecimientos.
Algunos autores proponen fabricar una medida de variación relativa que sea simétrica, esto es, que en el ejemplo anterior, tome los mismos valores pero con signos distintos. Por ejemplo, ello ocurre si definimos los crecimiengtos básicos como
![]()
esto es, si tomamos como medida del tamaño de la serie el promedio de los dos valores cuyos incrementos se evalúan. No obstante, esta medida no ha tenido mucho éxito en las aplicaciones prácticas, esto es, lo habitual es tomar en el denominador el valor anterior de la serie.
En principio, los crecimientos básicos debieran ser suficientes para evaluar el ritmo de variación de las series económicas. De hecho, cuando los datos son anuales, no suelen utilizarse otras tasas diferentes. Sin embargo, los fenómenos estacionales modifican la perspectiva, obligando a la introducción de otras tasas.
Veamos el siguiente ejemplo: Se proporcionan los últimos valores del IPC español, Grupo de Vestido y Calzado. La tabla inferior presenta también, en las tres últimas filas, los crecimientos básicos, crecimientos del índice con respecto al mes anterior.
IPC (base 2001) Vestido y calzado |
||||||||||||
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
|
2002 |
99.8 |
98.7 |
100.8 |
107.9 |
109.1 |
108.6 |
99 |
98.3 |
101.1 |
110 |
114.3 |
113.5 |
2003 |
102.6 |
101.8 |
104.7 |
113.8 |
115.1 |
114.5 |
102.8 |
102.1 |
105 |
113.2 |
116.9 |
116.3 |
2004 |
103.5 |
103 |
105.9 |
115.8 |
117.4 |
116.9 |
104.4 |
104 |
107.2 |
116.3 |
||
01
|
02
|
03
|
04
|
05
|
06
|
07
|
08
|
09
|
10
|
11
|
12
|
|
2002
|
-1.1 |
2.1 |
7.0 |
1.1 |
-0.5 |
-8.8 |
-0.7 |
2.8 |
8.8 |
3.9 |
-0.7 |
|
2003
|
-9.6 |
-0.8 |
2.8 |
8.7 |
1.1 |
-0.5 |
-10.2 |
-0.7 |
2.8 |
7.8 |
3.3 |
-0.5 |
2004
|
-11.0 |
-0.5 |
2.8 |
9.3 |
1.4 |
-0.4 |
-10.7 |
-0.4 |
3.1 |
8.5 |
||
 |
La figura que aparece en la derecha muestra la serie (en color naranja, escala derecha) y sus crecimientos básicos (color verde, escala izquierda). Nótese que los crecimientos básicos son muy importantes (a veces próximos al 10% de crecimiento ¡mensual!) en abril (final de las rebajas) y octubre (compras de ropa de otoño y la vuelta al cole). Por el contrario, las tasas son fuertemente negativas (del orden del -10%) en enero y julio (comienzo de las rebajas).
Si se quiere seguir el perfil de crecimiento, hace falta utilizar otras tasas, que complementan la visión de los crecimientos básicos. Las definiremos en este contexto (datos mensuales con periodicidad anual), aunque pueden servir para otras frecuencias y distintas periodicidades.
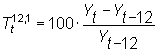
Nótese que no se ve afectada por la estacionalidad de la serie, ya que compara observaciones del mismo mes.
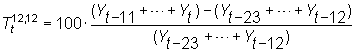
Como puede verse, es una tasa de variación de las medias móviles, o de las sumas móviles. Salva la estacionalidad, porque compara valores de un mes con los del mismo mes del año anterior, y salva las variaciones accidentales, por promediar términos, como se hace en la obtención de la componente tendencial.
Obsérvese que estas dos tasas están relacionadas, ya que
la tasa ![]() puede
escribirse como
puede
escribirse como
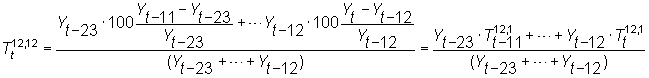
media ponderada de 12 tasas interanuales ![]() consecutivas.
consecutivas.
No vamos a entrar en estos materiales en un concepto que
se denomina "centrado de las tasas". Diremos
sólo que utilizando ese concepto, las tasas ![]() debieran
colocarse 6.5 meses antes (la calculada con datos de diciembre, debiera colocarse
el 15 de junio), y las tasas
debieran
colocarse 6.5 meses antes (la calculada con datos de diciembre, debiera colocarse
el 15 de junio), y las tasas ![]() 12
meses antes (la calculada con datos hasta diciembre, debiera colocarse el 1
de enero anterior).
12
meses antes (la calculada con datos hasta diciembre, debiera colocarse el 1
de enero anterior).
Aunque los crecimientos básicos y las dos tasas anteriores son las más utilizadas, hay otras dos que se manejan con frecuencia:
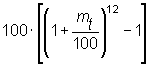
si los crecimientos básicos van expresados en porcentaje. Es la tasa de crecimiento anual que se obtendría si los 12 meses se creciera al ritmo del mes t-.ésimo. Como los crecimientos básicos, recoge muchas irregularidades, pero además las exagera, por lo que no la consideramos muy recomendable.
![]()
para h meses consecutivos, la tasa se calcula como
Pulsa aquí para encontrar una ilustración que te enseñará a calcular las tasas de una serie temporal.