VARIABLES CUANTITATIVAS

Característica cuyas modalidades son numéricas; por ejemplo: gastos, ingresos, edad, producción, etc. El hecho de que la variable tome muchos valores con pocas repeticiones (ingresos familiares, por ejemplo) o pocos valores con muchas repeticiones (número de hijos, por ejemplo) influye en el tipo de análisis a realizar; en el último caso, a la variable se le pueden aplicar los tratamientos estadísticos propios de los atributos ordinales.

Tablas de frecuencias. Tabla que recoge los valores de la variable y sus frecuencias, tanto en términos absolutos como relativos, estos últimos sin acumular y acumulados. Sólo tiene utilidad si la variable toma un número relativamente pequeño de valores distintos (número de hijos, número de días a la semana que una persona acude al cine,...).

Representaciones gráficas
Diagrama de barras. En un sistema de ejes cartesianos se levanta sobre el eje de abscisas una barra correspondiente a cada uno de los valores de la variable cuya altura sea igual a su frecuencia (absoluta o relativa).

 

Histograma de frecuencias. Esta es una de las representaciones gráficas más características en el caso en que las variables tomen muchos valores diferentes.

Cuando los valores de la variable se agrupan en intervalos de la misma amplitud, en un sistema de ejes cartesianos se levanta sobre cada intervalo un rectángulo de altura igual a la frecuencia (absoluta o relativa) del mismo.
Si los intervalos fuesen de distinta amplitud, se levantaría el rectángulo hasta una altura igual a , densidad de frecuencia del intervalo, , donde es la amplitud del intervalo i-ésimo; de esta forma el área de cada rectángulo es igual a la frecuencia del intervalo.

Función o curva de distribución. Representa sobre un sistema de ejes cartesianos los valores de la variable (en abscisas) y las frecuencias relativas acumuladas, (en ordenadas).

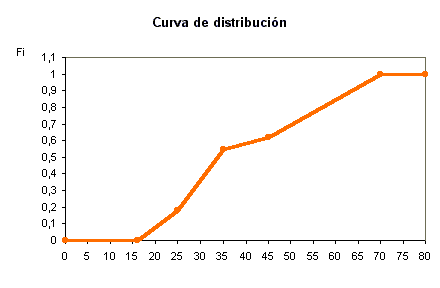Posteriormente, una vez considerados los resúmenes estadísticos, se verá otro gráfico de gran interés, el diagrama de caja

Resúmenes estadísticos: medidas de posición, dispersión y forma

Los resúmenes estadísticos reflejan numéricamente distintos aspectos de la característica en estudio. Las medidas de posición indican dónde se encuentra el centro u otra zona de la distribución. Las medidas de dispersión cuantifican la distancia de los datos entre sí o respecto de una medida de posición central y las medidas de distribución o forma describen numéricamente el perfil de la distribución en cuanto a su asimetría y apuntamiento; estas medidas, salvo contadas excepciones, sólo son aplicables a características cuantitativas. En el caso particular en que las variables estén agrupadas en clases o intervalos, todos los resúmenes se calcularán a partir de las marcas de clase (punto medio del intervalo).

Medidas de posición
Si se considera , los valores de X para cada uno de los N individuos,

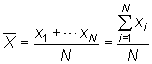
Si se considera , los posibles valores distintos, y el número o la proporción de repeticiones de cada valor, y, respectivamente

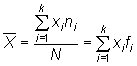
La media es el valor de reparto igualitario: la renta media familiar es la renta que tendría cada familia si a todas les correspondiese la misma renta.

La media se considerará un buen resumen del centro de la distribución cuando no existan valores "raros", esto es, valores significativamente distintos de los demás, y cuando la distribución presente poca dispersión.

Mediana
La mediana, que se designará por Me, es el valor que divide en dos partes “iguales” la distribución de frecuencias; esto es, valor Me que verifica:
- Porcentaje de valores menores o iguales que
- Porcentaje de valores mayores o iguales que
La mediana es el verdadero valor central: la “mitad” de las familias tiene rentas inferiores o iguales a la renta mediana y la otra “mitad” rentas superiores o iguales a la renta mediana.

Moda
La moda es el valor (o modalidad en el caso de características cualitativas) al que le corresponde la mayor frecuencia.

Media recortada
Media aritmética de un cierto porcentaje de observaciones centrales de la variable. Así, la media recortada al k% es el promedio de los valores una vez excluidos el k% de los valores más pequeños y el k% de los valores más grandes.
La media aritmética es una medida muy sensible a la presencia de observaciones extrañas o atípicas (outliers); las medias recortadas, al igual que la mediana, son una alternativa a la media aritmética en estas situaciones.

Cuantiles
Valores de la variable que dividen su distribución en partes que contienen el mismo número de observaciones. Los más habituales son los que dividen a la distribución en cuatro partes, cuartiles, en diez partes, deciles, o en cien partes, percentiles. Así, por ejemplo,
C1 , primer cuartil, deja por detrás el 25% y por delante el 75% de las observaciones.
d3 , tercer decil, deja por detrás el 30% y por delante el 70% de las observaciones.
p47 , cuadragésimo séptimo percentil, deja por detrás el 47% y por delante el 53% de las observaciones.
Estas medidas ordenan a un individuo en la distribución: una familia que está en el percentil 66 de renta tiene una renta mayor o igual que el 66% de las familias o, en sentido contrario, tiene una renta inferior o igual al 34% de las familias.

Medidas de dispersión

Varianza
Si se considera , los valores de X para cada uno de los N individuos,

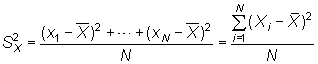
Si se considera los posibles valores distintos, y el número o la proporción de repeticiones de cada valor, y ,

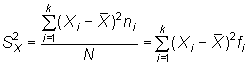
La varianza mide la dispersión de los valores de la variable respecto de su media, de hecho, es la media de las desviaciones respecto de la media al cuadrado.
En el mundo anglosajón, se define la varianza como

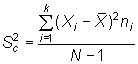
medida que se suele denominar cuasivarianza.

La raíz cuadrada positiva de la varianza es la desviación típica o estándar (cuasidesviación en el caso de la cuasivarianza).

La varianza o, preferiblemente, la desviación típica nos dan una idea de la representatividad de la media: cuanto menor sea la dispersión existente entre las observaciones mayor será la representatividad de la media.

No obstante, tanto la varianza como la desviación típica son medidas que dependen de las unidades de medida de la variable, esto es, de su tamaño. Así, por ejemplo, una varianza de 13,8 puede suponer mucha dispersión en una variable del tipo número de hijos pero no así en una variable como las ventas mensuales en euros de una gran superifice. Por esta razón, cuando estemos interesados en saber hasta qué punto una media es un buen resumen de un conjunto de datos o queramos comparar la representatividad de dos o más medias, utilizaremos la medida de dispersión relativa que se define a continuación.

Coeficiente de variación de Pearson

Este coeficiente se suele leer en porcentaje y se interpreta como el porcentaje que representa la desviación típica sobre la media.

Valores grandes de este coeficiente indican una alta dispersión relativa, es decir, la desviación es grande en relación a la media y, en consecuencia, ésta no será muy representativa del conjunto de observaciones; por el contrario, valores bajos suponen poca dispersión relativa con lo que la media será resumirá razonablemente bien el centro de la distribución.

Máximo, mínimo y rango
Menor valor observado (mínimo), mayor valor (máximo) y diferencia entre ambos (rango, amplitud o recorrido). También se pueden calcular rangos entre percentiles, por ejemplo, el rango intercuartílico .

Medidas de distribución o forma

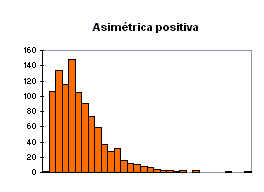
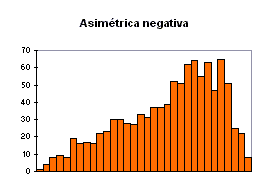
Coeficiente de asimetría

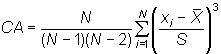
donde S es la cuasidesviación típica. Si CA es positivo, revela asimetría hacia la derecha, es decir, la distribución presenta una cola alargada hacia los valores altos de la variable; si es negativo, la distribución presenta asimetría hacia la izquierda, y si es próximo a cero, la distribución es más o menos simétrica. Los gráficos siguientes ilustran las tres situaciones

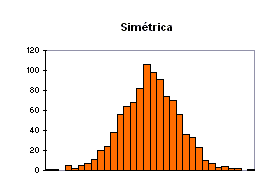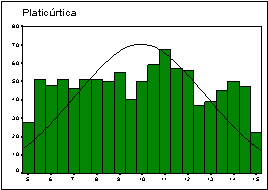
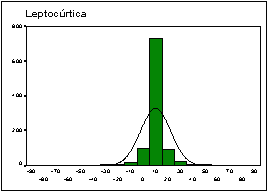
Coeficiente de curtosis

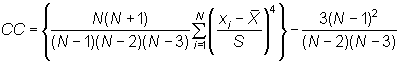
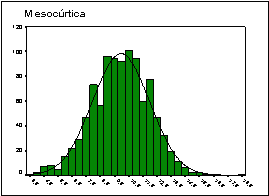
donde S es la cuasidesviación típica. Si CC es positivo, la distribución (su histograma) es más apuntada (leptocúrtica) que la distribución normal de la misma media y varianza; si es negativo, es más aplastada (platicúrtica) y si es próximo a cero, presenta un perfil similar (mesocúrtica).

En la hoja adjunta se muestra un análisis descriptivo básico de una variable con pocos valores diferentes (discreta) y otra con muchos valores diferentes (continua).

El diagrama de caja

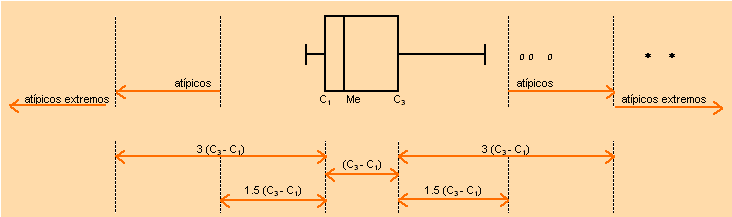
El diagrama de caja es una representación gráfica basada en los cuartiles que permite estudiar la posición, la dispersión y la simetría de la distribución e identificar los posibles valores atípicos, es decir, aquellas observaciones que son sensiblemente diferentes (por extremadamente grandes o extremadamente pequeñas) de las demás.
Para construir un diagrama de caja se siguen los siguientes pasos:
- Ordenar las observaciones en sentido creciente y determinar el valor mínimo, el máximo y los tres cuartiles, , y .
- Dibujar la caja, un rectángulo cuyos extremos sean los cuartiles primero y tercero, y dividirlo con una línea vertical a la altura de la mediana.
- Calcular los límites mínimo y máximo a partir de los cuales se van a considerar las observaciones como atípicas. Estos limites se calculan de la siguiente manera:

- Dibujar unas líneas que vayan desde cada extremo de la caja hasta el último valor de la variable no atípico, es decir, que se encuentre dentro del intervalo (LI, LS).
- Señalar los valores atípicos con un símbolo (por ejemplo un círculo); a veces, se distingue entre atípicos y atípicos extremos, según se alejen de LI y LS, respectivamente, menos o más de .

La utilización de la mediana como medida de centralización y del recorrido intercuartílico como medida de dispersión se explica porque estas medidas, al depender del orden de los datos y no de su magnitud, son poco sensibles a la presencia de observaciones atípicas. En la hoja adjunta se incluye un ejemplo de este tipo de representación gráfica.