MEDIDAS DE CONCENTRACIÓN

Para resumir la información de un conjunto de datos, la Estadística Descriptiva proporciona una serie de medidas que se clasifican de acuerdo con el tipo de características que se quieran poner en evidencia. Así, hablamos de medidas de posición, dispersión, forma y, por último, de medidas de concentración.

Mientras que las primeras se pueden aplicar a cualquier variable estadística, estas últimas, que desarrollaremos en el presente tema, sólo pueden ser aplicadas a las variables que toman valores positivos. La condición anterior es necesaria desde el punto de vista formal, pero insuficiente en cuanto a su significado.

Las medidas de concentración han de aplicarse a variables en las que tenga sentido plantearse la consideración del grado de reparto entre cada uno de los individuos de la suma total de los valores de la variable (como siempre en Estadística, entenderemos la palabra individuo de forma genérica, es decir, las unidades de las cuales se observa una cierta característica).

Las medidas de concentración son medidas de reparto del total de la variable. Trataremos de estudiar si el reparto es más o menos equitativo (el total se reparte de forma más o menos igualitaria entre los individuos) o desigual (unos pocos individuos concentran en sí gran parte del total).

De lo anterior ya podemos deducir qué variables serán aquellas susceptibles de ser medidas desde el punto de vista de la concentración: rentas de personas, regiones o países, ingresos y gastos familiares, ventas de las empresas de un sector económico, propiedades agrícolas, población provincial o regional, etc.

Situemos el problema en su génesis histórica. Desde sus orígenes, la Economía ha tratado de explicar el porqué de las desigualdades entre las distintas naciones o entre los individuos de una de ellas. En este afán una de las primeras tareas ha consistido en la medición de esa desigualdad manifiesta. Los enfoques han sido y son múltiples. El que aquí vamos a ver y que se conoce en toda la literatura estadística con el nombre de medidas de concentración, recoge técnicas de medición del reparto de la renta (y por extensión de otro tipo de variables) que tienen su origen en la curva de Lorenz. En 1905, el estadístico americano Max Lorenz propone un método gráfico para medir el grado de concentración (o de distribución) del total de la renta de un país entre sus ciudadanos.

La idea es muy simple: para un cierto nivel de renta, se compara el porcentaje de individuos con rentas iguales o inferiores a la dada y el porcentaje de renta que dichos individuos detentan. Realizada esta comparación para distintos niveles de renta, si los pares de porcentajes obtenidos son parecidos, la renta estará distribuida más o menos equitativamente; si, por el contrario, estos pares de porcentajes difieren sustancialmente, la renta presenta una distribución poco igualitaria, concentrándose en manos de unos pocos.

Acudiendo al símil vulgar, pero siempre esclarecedor, de la tarta, las medidas de concentración calibran el buen o mal reparto del pastel.

Planteemos el problema con un ejemplo que recoja la distribución del salario mensual, en euros, de los empleados de la empresa LOGISA.

Organizaremos en una tabla los cálculos para hallar (proporción de empleados con salarios iguales o inferiores a uno dado) y (proporción de masa salarial acumulada por dichos empleados). Si los datos de la variable, referidos a N individuos, están agrupados en k intervalos (cuando los datos estén sin agrupar el planteamiento es idéntico) dicha tabla incluirá:
, intervalo de valores de la variable X (salarios, rentas,...).

, marca de clase (valor medio del intervalo), que representará a todos los valores incluidos en el mismo.
, número de individuos para los cuales la variable X toma valores en el intervalo.
, número de individuos para los cuales X toma valores iguales o inferiores al extremo superior del intervalo, .
, valor anterior expresado en proporción sobre el total de individuos.
, suma total de los valores de X para los individuos del intervalo.
, suma total de los valores de X para los individuos en los que X toma valores inferiores o iguales a .
, valor anterior expresado en proporción sobre la suma total S de la variable.

Para los datos salariales de la empresa LOGISA, el cuadro obtenido será:

La tabla se interpretará de la siguiente forma. Si nos fijamos, por ejemplo, en la fila correspondiente al tercer intervalo salarial, sabremos que el 82% de los empleados de salarios inferiores (los 225 que no superan los 1.500 €) acumulan el 62% de la masa salarial (en concreto 204.250 euros).
La observación de la discrepancia entre las columnas con los valores y nos puede dar una primera idea del grado de reparto del "pastel", en este caso, de los 330.500 euros que constituye la masa salarial mensual de la empresa LOGISA. Pero la observación, sin más, puede llevar a distintas interpretaciones. Un observador puede decir que dichas columnas se parecen mucho, mientras que otro puede opinar lo contrario. La Estadística proporciona medidas objetivas de la discrepancia entre y , es decir, medidas objetivas del reparto de la masa salarial.
A continuación se muestran dos de estas medidas: una gráfica, la curva de Lorenz y otra geométrica, el índice de Gini.
Max Lorenz propuso la primera medida, de la que se deduce el resto. Sobre un sistema de ejes cartesianos se representan los pares de valores , ,,..., donde el último par será siempre (1,1). La poligonal obtenida al unir dichos puntos mediante segmentos recibe el nombre de curva de Lorenz. Para resaltar más la representación se enmarca el sistema de ejes en un cuadrado de lado unidad con uno de los vértices en el origen (obsérvese que todos los y están comprendidos entre 0 y 1), trazando la diagonal del mismo.
Para los valores de la empresa LOGISA la curva de Lorenz será:

Cuando los salarios presenten una distribución más o menos igualitaria, los valores de y serán similares. Por tanto, la curva de concentración tenderá a acercarse a la diagonal (los puntos de la diagonal tienen el mismo valor de abscisa y ordenada).
Cuando los salarios presenten una distribución muy desigual, tendiendo a concentrarse la masa salarial en unos pocos empleados, los valores de y serán muy dispares. Entonces la curva se alejará de la diagonal.
Veamos qué ocurre en los dos casos extremos:
Equidistribución
El total de valores de la variable S, se distribuye en partes iguales entre los N individuos, correspondiendo S/N a cada uno. Entonces el cuadro quedará:

S/N	N	N	1	S	S	1

La curva de Lorenz coincidirá con la diagonal:

 

Máxima concentración
Uno de los individuos acapara el valor total S de la variable.

0	N-1	N-1	(N-1)/N	0	0	0
S	1	1	1	S	S	1

Entonces la curva quedará "casi" pegada a los lados del recuadro:

Por tanto, en la medida en que la curva se acerque a la diagonal, hablaremos de equidistribución, y en la medida en que se aleje, hablaremos de concentración.
La curva de Lorenz, como medida de concentración, presenta un problema debido a su naturaleza gráfica. Cuando se interpreta para una única distribución entramos en valoraciones subjetivas en relación al acercamiento o alejamiento de la curva a la diagonal; cuando comparamos dos distribuciones, a veces es difícil apreciar cuál de las dos curvas se "pega" más a la recta de equidistribución.
Para evitar este inconveniente se desarrolla otro tipo de medidas, unas geométricas y otras analíticas.

En el año 1912 el estadístico y demógrafo italiano Corrado Gini propone una medida de concentración en base a la curva de Lorenz, que consiste en una medición numérica del grado de acercamiento de la curva a la recta de equidistribución: el área entre dicha curva y la diagonal, que llamaremos área de concentración, Ac. Entonces se define el índice de Gini como el doble de dicho área:

El cálculo de este índice, en concreto del área de concentración, se realiza de forma sencilla teniendo en cuenta las áreas del triángulo y trapecios que quedan por debajo de la curva de Lorenz.
Para los salarios de LOGISA, este índice vale 0,285.
De cara a interpretar dicho valor consideremos de nuevo los casos extremos:

Equidistribución

(En buena lógica no estaría definido).

Máxima concentración

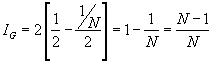
Dicho valor será prácticamente uno cuando el número de individuos N sea lo suficientemente grande.
De esta forma, valores del índice próximos a cero indican repartos igualitarios y valores próximos a uno repartos desiguales.

La mediala
A partir de la curva de concentración de Lorenz se puede definir una característica que, comparándola con la mediana, permite medir el grado de reparto de la suma total de valores de la variable (S).
La mediala (Md) es el valor de la variable tal que la suma de los valores de los individuos que individualmente toman un valor inferior o igual a la mediala, es igual a la suma de los valores de los individuos que individualmente toman un valor mayor que la mediala. Así, la mediala es el valor de la variable para el cual toma el valor 0.5. Si, cuando calculamos los pares de puntos (, ) que determinan la curva de concentración, existe un valor de exactamente igual a 0.5, la mediala será el extremo superior del intervalo correspondiente. Si no es así, y al igual que ocurría con la mediana, la mediala se obtendrá por interpolación lineal entre los extremos del intervalo medial (aquel al que le corresponda el valor de inmediatamente superior a 0.5).
En el caso extremo de equidistribución, la mediala coincidirá con la mediana: "la mitad de los individuos se lleva la mitad del pastel". En los demás casos, la mediala será superior a la mediana: "la mitad de los individuos, los que toman los valores inferiores de la variable, se reparte menos de la mitad del pastel". La discrepancia entre la mediana y la mediala da una idea del grado de concentración de las dos mitades del total de valores de la variable.

Cálculo de la mediala para la empresa LOGISA
Como se observa en la tabla que recoge los cálculos realizados para la determinación de la curva de Lorenz para la empresa LOGISA, no existe ningún valor de igual a 0.5. El intervalo (1000, 1500] es aquel al que le corresponde un valor de inmediatamente superior a 0.5; esto es, se trata del intervalo medial. Interpolando en él, calcularemos la mediala:

De acuerdo con el resultado anterior, los trabajadores que individualmente reciben un salario menor o igual a 1277,14 euros, se llevan conjuntamente la mitad de la masa salarial, esto es, 165.250 euros.
Una vez determinada la mediala podremos conocer qué porcentaje de individuos gana menos que la mediala, o lo que es lo mismo, se reparte el 50% de la masa salarial.
En nuestro ejemplo,

Este valor indica que el 70% de los trabajadores que menos ganan se llevan el 50% de la masa salarial, mientras que el 30% restante (los mejor pagados) se reparte la otra mitad.

Para ver resolución del ejemplo LOGISA pulsa aquí. Para ver otro ejemplo pulsa aquí.