,
de la que se dispone de una muestra de tamaño n. Entonces,
la proporción poblacional p no es otra cosa que la media poblacional
de dicha variable, estimándose con la correspondiente proporción
muestral o media muestral, 
.Contrastes de proporciones
En la inferencia sobre una proporción
el problema se concreta en estimar y contrastar la proporción p de
individuos de una población que presentan una determinada
característica A (proporción de votantes a un partido
político, proporción de parados, ...). El problema se modeliza
mediante una variable dicotómica que toma el valor 1 si se presenta
la característica de interés y 0 en caso contrario, esto es,
una variable de Bernoulli, ,
de la que se dispone de una muestra de tamaño n. Entonces,
la proporción poblacional p no es otra cosa que la media poblacional
de dicha variable, estimándose con la correspondiente proporción
muestral o media muestral, .
 |
En el caso de dos poblaciones,
se trata de comparar la proporción en la que se presenta una cierta
característica A en las mismas (comparar la proporción
de voto a un partido en dos regiones, comparar la proporción de parados
entre hombres y mujeres, ...). El problema se modeliza mediante dos variables
de Bernoulli independientes, de las que se dispone de sendas muestras aleatorias
de tamaño 
y 
, respectivamente.
 |
| Proporciones | Una población | C. de H. sobre la proporción poblacional |
| Dos poblaciones | C. de H. sobre la diferencia de proporciones poblacionales | |
Contraste de hipótesis sobre la proporción poblacional
A partir del estadístico, S, número de individuos de la muestra que presentan la característica A,
 |
se pueden construir los siguientes contrastes
de hipótesis a nivel de significación 
:
a) Bilateral
 |
Teniendo en cuenta el estadístico
bajo 
, se rechaza
esta hipótesis cuando
 |
siendo a y b los
valores que en la distribución 
dejan
en cada cola una probabilidad no superior a 
.
Esto es, se rechaza cuando
hay discrepancias significativamente grandes entre el número de individuos
de la muestra que presentan la característica A, S, y
el número esperado bajo , 
.
Además,
 |
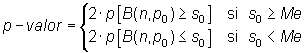donde 
es
el valor muestral del estadístico
y Me la mediana de la correspondiente distribución binomial.
b) Unilateral
 |
Teniendo en cuenta el estadístico
bajo , se rechaza
esta hipótesis cuando
 |
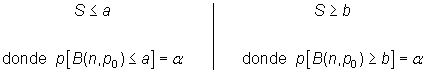Además,
 |
donde es
el valor muestral del estadístico.
Los contrastes también se pueden obtener a partir del estadístico
Contraste de hipótesis sobre la diferencia de proporciones poblacionales
A partir del estadístico
 |
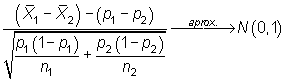se pueden construir los siguientes
contrastes de hipótesis a nivel de significación :
Bilateral
 |
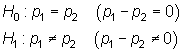Teniendo en cuenta el estadístico
bajo , se rechaza
esta hipótesis cuando
 |
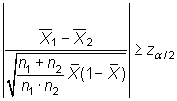siendo 
la
estimación de la proporción
bajo , 
,
con las dos muestras conjuntamente y 
el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de .
El estadístico mide la discrepancia entre la
diferencia de proporciones muestrales, observadas o empíricas, 
,
y la diferencia de proporciones poblacionales, esperadas o teóricas
bajo ,
: discrepancias
significativamente grandes llevan a
rechazar .
Además,
 |
siendo 
el
valor muestral del estadístico.
En el mismo sentido que este contraste de diferencia de proporciones igual a cero (igualdad de proporciones), se pueden construir contrastes de diferencia de proporciones igual a d.
El test admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de estos contrastes.
