,de
la que se dispone de una muestra de tamaño n.
Entonces, la proporción
poblacional p no
es otra cosa que la media poblacional de dicha variable, estimándose con la correspondiente
proporción muestral o media muestral, 
.Intervalos de confianza para proporciones
En la inferencia sobre una proporción
el problema se concreta en estimar y contrastar la proporción p de
individuos de una población que presentan una determinada
característica A (proporción
de votantes a un partido político, proporción de parados, ...).
El problema se modeliza mediante una variable dicotómica que toma el
valor 1 si se presenta la característica de interés y 0 en caso
contrario, esto es, una variable de Bernoulli, ,de
la que se dispone de una muestra de tamaño n.
Entonces, la proporción
poblacional p no
es otra cosa que la media poblacional de dicha variable, estimándose con la correspondiente
proporción muestral o media muestral, .
 |
En el caso de dos poblaciones,
se trata de comparar la proporción
en la que se presenta una cierta característica A en las mismas
(comparar la proporción de voto a un partido en dos regiones, comparar la proporción
de parados entre hombres y mujeres, ...). El problema se modeliza mediante
dos
variables
de
Bernoulli
independientes,
de
las
que
se
dispone de
sendas
muestras
aleatorias
de tamaño 
y 
,
respectivamente.
 |
| Una población | I. de C. sobre la proporción poblacional | |
| Proporciones | ||
| Dos poblaciones | I. de C. sobre la diferencia de proporciones poblacionales | |
Intervalo de confianza sobre la proporción poblacional
A partir del estadístico
 |
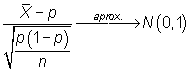se construye el intervalo
 |
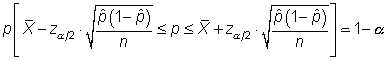siendo 
el
valor que en una distribución normal estándar
deja a su derecha una probabilidad de 
.
Véase en la hoja adjunta un ejemplo.
Cuando se va a realizar una encuesta para estimar una proporción, lo habitual es plantearse a priori obtener una cierta fiabilidad y precisión en la estimación, buscando el tamaño muestral necesario para conseguirlas. La longitud del intervalo de confianza para p resulta:
 |
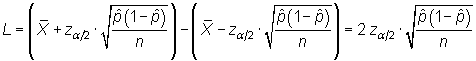De aquí podremos calcular el valor
de n en función de la longitud
del intervalo, L, y de su fiabilidad, 1-
:
 |
Adviértase que llegamos a un resultado en principio incongruente: queremos saber cuántas observaciones tenemos que realizar para estimar p y para ello necesitaremos conocer su estimación, valor que conoceremos una vez hayamos realizado las observaciones. ¿Cómo solucionar este problema? Existen tres posibles vías:
a) Si tuviésemos información (encuestas anteriores, opiniones de experto,...) sobre el posible valor de la proporción a estimar, sustituiríamos este valor en la anterior expresión.
b) Podríamos realizar una pequeña encuesta (encuesta piloto) que nos proporcionase una primera evaluación de la proporción muestral. Además, esta encuesta puede servir para probar y reformar el cuestionario, organizar el trabajo de campo, etc.
c) Si no contásemos con información alguna ni tuviésemos la posibilidad de realizar la encuesta piloto, nos pondríamos en la situación más desfavorable, esto es, la que da lugar al tamaño muestral más grande para la fiabilidad y precisión deseadas. Esa situación se produce cuando n alcanza su máximo, lo cual ocurre cuando p=q=0.5.
En este caso, por otro lado el más habitual, resulta:
 |
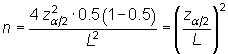En la hoja adjunta se obtiene el tamaño muestral para una fiabilidad y una precisión determinada en el caso más desfavorable (p=q=0.5).
Intervalo de confianza sobre la diferencia de proporciones poblacionales
A partir del estadístico
 |
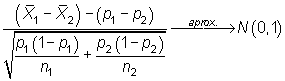se construye el intervalo
 |
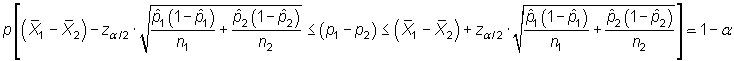siendo el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de .
Véase en la hoja adjunta un ejemplo.
