Método de los momentos (de analogía)
El método de los momentos esta basado en una idea clásica
que propone estimar las medias o varianzas poblacionales mediante las medias
o varianzas muestrales, respectivamente. Por ello se denomina de analogía,
porque su técnica consiste en sustituir las características poblacionales por
las análogas muestrales.
El razonamiento básico que apoya este método es que si la
muestra es representativa de la población, las características muestrales deberán
ser representativas de las poblacionales.
La mayor ventaja de este método es su sencillez de aplicación,
por lo que se sigue utilizando en situaciones en las que otros métodos se complican,
o cuando el número de parámetros desconocidos a estimar es abundante.
No obstante, los estimadores obtenidos por este método no
están muy cualificados.
- Por un lado, no gozan de propiedades especialmente buenas.
- Además, no proporcionan resultados unívocos, sino que el
mismo método puede conducir a resultados muy diferentes.
- Finalmente, a veces ni siquiera proporciona estimadores,
esto es, las estimaciones pueden no ser valores posibles de los parámetros.
Definamos el método y más adelante iremos viendo todas estas
objeciones.
Sea 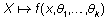 una
población cuya densidad
o función de probabilidad depende de k parámetros desconocidos.
Sus momentos, una
población cuya densidad
o función de probabilidad depende de k parámetros desconocidos.
Sus momentos, 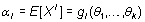 ,
dependerán de los parámetros, por lo que podemos escribir el sistema
de k ecuaciones con k incógnitas ,
dependerán de los parámetros, por lo que podemos escribir el sistema
de k ecuaciones con k incógnitas
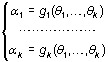
que puede resolverse con respecto a
los parámetros,
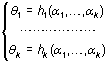
Entonces, dada una muestra aleatoria
simple, 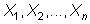 ,
los estimadores por el método de los momentos se obtienen sustituyendo ,
los estimadores por el método de los momentos se obtienen sustituyendo
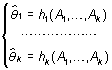
donde 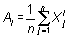 es
el momento muestral de orden i-ésimo. es
el momento muestral de orden i-ésimo.
|
La elección de los k primeros momentos, y
el hecho de que sean centrados respecto del origen (no centrales) es una simplificación.
La idea es elegir aquellos momentos que simplifiquen más la resolución del
sistema de ecuaciones y, por otro lado, que sean fáciles de calcular (del menor
orden posible). Nótese también que las ecuaciones del sistema no son lineales,
por lo que no está garantizado que el sistema tenga solución.
El Ejemplo5 ilustra
este método. Por otro lado, el Ejemplo6 ilustra
de manera sencilla la no univocidad
de la solución. En el Ejemplo7 se muestra
su uso en la estimación de proporciones para situaciones difíciles que producen
sesgos de respuesta.
![]() una
población cuya densidad
o función de probabilidad depende de k parámetros desconocidos.
Sus momentos,
una
población cuya densidad
o función de probabilidad depende de k parámetros desconocidos.
Sus momentos, ![]() ,
dependerán de los parámetros, por lo que podemos escribir el sistema
de k ecuaciones con k incógnitas
,
dependerán de los parámetros, por lo que podemos escribir el sistema
de k ecuaciones con k incógnitas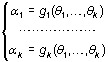
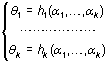
![]() ,
los estimadores por el método de los momentos se obtienen sustituyendo
,
los estimadores por el método de los momentos se obtienen sustituyendo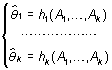
![]() es
el momento muestral de orden i-ésimo.
es
el momento muestral de orden i-ésimo.