Estimadores insesgados

1. Obsérvese que escribimos el sesgo de un estimador con la letra "b", en lugar de la letra "s", como parecería más normal. Esto ocurre porque, como sabemos, la letra "s" se emplea para designar la desviación típica de unos datos (de una muestra). En su lugar, se emplea la inicial de la palabra "biais" (léase bié), que es la expresión francesa para sesgo.
2. El sesgo de un estimador es un número, que depende del valor del parámetro, q. Por tanto, es una función del parámetro. En efecto, como veremos en los siguientes ejemplos, la esperanza del estimador, es una función del parámetro porque la función de densidad o de probabilidad del estimador depende del mismo. En consecuencia el sesgo depende también de q.
3. Un estimador insesgado (con sesgo nulo) tiene por esperanza el valor del parámetro, sea quien sea éste. Por ello, a los estimadores insesgados se les denomina también centrados. Nótese que si utilizamos un estimador insesgado, "acertamos" en media, esto es, el valor esperado del estimador es la cantidad que queremos estimar.
4. Ello no quiere decir, no obstante, que las estimaciones (que son los valores que toma el estimador) se parezcan al parámetro, por el mismo motivo que una variable de Bernoulli b(p), tiene por esperanza p, aunque sus valores son cero y uno. En otras palabras, una variable aleatoria no tiene por qué estar cerca de su esperanza, luego un estimador insesgado no tiene por qué estar cerca del parámetro.
5. Obsérvese, finalmente, que se habla de estimadores insesgados. Esta propiedad no se aplica a las estimaciones, esto es, no tiene sentido decir que una estimación es o no es insesgada.

Observa qué ocurre con los estimadores anteriores en la continuación del Ejemplo1 y en la continuación del Ejemplo2

¿Conviene utilizar estimadores insesgados? o, dicho de otra forma, la insesgadez, ¿es una propiedad de interés para los estimadores?

En esta ilustración se muestra la función de densidad de dos estimadores de q. es la densidad de un estimador insesgado, , mientras que es la de un estimador sesgado, .

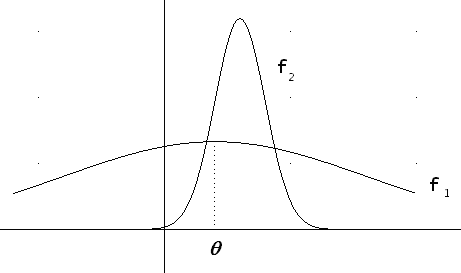Pero puede observarse que aunque el estimador sea sesgado, asigna mayores probabilidades que a los valores próximos a q , esto es, resulta más probable que las estimaciones obtenidas con se encuentren más próximas al parámetro que las obtenidas con .

Dicho de otra forma, la propiedad interesante para un estimador es su proximidad al parámetro, sea éste su esperanza o no lo sea. Una forma de valorar esta proximidad es a través de la dispersión cuadrática, del estimador con respecto al parámetro, denominada error cuadrático medio.

Error cuadrático medio. Estimadores insesgados de varianza mínima

No es difícil demostrar esa descomposición del error cuadrático medio. Obsérvese que

(donde estamos llamando a la esperanza del estimador). Entonces, el error cuadrático medio (esperanza del término de la izquierda) es la suma de tres esperanzas:

• es la varianza del estimador,
• es el cuadrado del sesgo del estimador, y
• ya que la esperanza de una variable menos su esperanza es siempre igual a cero.

Es interesante observar que, entonces, para calcular el error cuadrático medio basta con calcular (o conocer) los dos primeros momentos, esperanza y varianza, del estimador.

Obsérvese asimismo que, al depender de q la distribución del estimador, también dependen del parámetro su esperanza y varianza y, por tanto, el error cuadrático medio. Por tanto, este error es no aleatorio, aunque depende del valor (desconocido) de q .

El error cuadrático medio nos permite comparar estimadores. Así, un criterio sería concluir que entre dos estimadores, es preferible aquél cuyo error cuadrático medio es menor. Este criterio se denomina de eficiencia relativa:

Nuevamente, la continuación del Ejemplo1 y la continuación del Ejemplo2 ilustran estas ideas

Aunque el error cuadrático medio nos proporciona una forma de comparar estimadores, no permite obtener estimadores óptimos. Esto es, para un problema concreto, no es posible obtener el estimador de menor error cuadrático medio entre todos los estimadores del parámetro. Por ello esta propiedad (la de minimizar el error cuadrático medio) no se suele presentar entre las propiedades convenientes de los estimadores, porque no tiene interés práctico.

Si limitamos nuestro campo de interés a los estimadores insesgados, a veces el problema tiene solución práctica. Para los estimadores insesgados, el error cuadrático medio coincide con la varianza, por lo que hablaremos de estimadores insesgados de varianza mínima.

Estimadores insesgados de mínima varianza

Los estimadores insesgados de mínima varianza no tienen por qué existir para un problema concreto. Pero si existen son únicos, esto es, para un problema concreto, no pueden existir dos estimadores insesgados de varianza mínima distintos.

En efecto, supongamos que hubiera dos estimadores insesgados de mínima varianza, y . Vamos a concluir que tienen que ser el mismo, esto es, que tienen que ser iguales.

Como los dos son insesgados, , y como ambos son de mínima varianza, los dos tendrén la misma varianza, V, esto es,

Pensemos en otro estimador, en concreto, el promedio de los dos anteriores, . Como promedio de dos estimadores insesgados será también insesgado,

Su varianza, que vale

no puede ser menor que V, ya que entonces y no serían de mínima varianza entre los insesgados. Por tanto,

y, por tanto, . Pero esta desigualdad implica entonces que

y como los coeficientes de correlación lineal no pueden ser superiores a la unidad, deberá ser . Pero entonces existe una relación lineal entre ambos estimadores, , con b mayor o igual que cero, ya que el coeficiente de correlación es positivo. Veremos que a=0 y b=1. Tomando varianzas en esta expresión,

de donde , esto es, b=1, ya que es positivo. Pero entonces, tomando esperanzas,

o, lo que es lo mismo, a=0 . En definitiva, a=0 y b=1, y por tanto, . Si existen dos estimadores insesgados de mínima varianza son, necesariamente, iguales.

En conclusión, para un problema concreto, puede que exista o puede que no exista un estimador insesgado de mínima varianza, y si existe, es único. Pero, ¿cómo localizarlo si existe? Como veremos a continuación,

1. Sólo es posible intentar obtenerlo en ciertos problemas, cuando se cumplan unas condiciones de regularidad que se denominan de Cramér-Rao.
2. En esos problemas, sólo se puede localizar si pertenece a cierto tipo de estimadores insesgados de mínima varianza, los denominados estimadores eficientes.

Condiciones de regularidad de Cramér-Rao

Sea una población, una m.a.s. de X. Decimos que se cumplen las condiciones de regularidad de Cramér-Rao si se cumple:

1. , esto es, el campo de variación de la población es el mismo para cualquier valor, q, del parámetro.
2. El campo de variación del parámetro, esto es, el conjunto Q, es un intervalo abierto de la recta real.
3. Para cualquier y para cualquier , existe , excepto, tal vez, para un conjunto de puntos de probabilidad nula.
4. Se cumple que
5. La esperanza existe y es mayor que cero para todo .
6. Si es un estimador insesgado,

La primera de las condiciones no se verifica en situaciones de interés. Por ejemplo, si X, una renta de una población, tiene la distribución de Pareto, y q es la renta mínima, se obtiene , esto es, X varía entre q e infinito. Si la población es uniforme , entonces , que depende de q . Por el contrario, si la población es normal , esto es, q es la media poblacional normal, que no depende de q .

En cuanto a la segunda condición, aunque habitualmente el campo de variación del parámetro es un intervalo, con cierta frecuencia incluye a los bordes, esto es, Q es un intervalo cerrado. Por ejemplo, si , esto es, p es la probabilidad de éxito a estimar, el campo de variación de p es el intervalo [0,1], que no es abierto, porque incluye a sus bordes, 0 y 1. Pero estos valores indican que el éxito ocurre siempre (p=1) o bien no ocurre nunca (p=0), valores que pueden analizarse habitualmente por otros medios, por lo que, cuando nos planteamos este problema de estimación, puede suponerse que el campo de variación es el intervalo abierto (0,1)

En cuanto al resto de condiciones, la cuarta y la sexta garantizan que ciertas derivadas con respecto al parámetro se pueden realizar bajo el signo integral, mientras que la tercera y la quinta son condiciones de derivabilidad y de no anulación. Si bien es necesario exigir estas condiciones de regularidad, en nuestro trabajo se verifican siempre, y son raros los ejemplos en que no se cumplen, ninguno de ellos referentes a distribuciones poblacionales habituales. Por ello daremos por supuesto que se verifican siempre, y no las comprobaremos. Dejemos escrito este acuerdo:

Puede el lector comprobar en la siguiente tabla cuándo se verifican estas condiciones para distribuciones muy utilizadas.

Cuando se cumplen las condiciones de regularidad de Cramér-Rao, es posible obtener una cota inferior de la varianza de los estimadores insesgados, lo que nos ayudará a resolver el problema planteado. El resultado se denomina Desigualdad de Cramér-Rao.

Desigualdad de Cramér-Rao

Este resultado, que no demostraremos [enlace o capa con la demostración] proporciona, como puede verse, una cota inferior de las varianzas de todos los estimadores insesgados. Dicha cota, no depende del estimador, sino sólo de q y del tamaño de la muestra, n.

Dicho de otra firma, si se cumplen las condiciones de regularidad, las varianzas de los estimadores insesgados son todas mayores o iguales que la cota de Cramér-Rao.

¿Qué ocurre entonces si existe un estimador insesgado cuya varianza coincide con dicha cota, esto es, un estimador con y ? Como no puede haber un estimador insesgado con varianza menor que la cota de Cramér-Rao, será insesgado de mínima varianza. Se dice de él que es un estimador eficiente, una categoría dentro de los estimadores insesgados de mínima varianza. Puede verse la definición e interés pulsando en el enlace correspondiente a los estimadores eficientes.