Convergencias y Teorema del Límite Central

Convergencias
Ley débil de los grandes números
Teorema del Límite Central

 

Denominamos sucesión de variables aleatorias, ,a la sucesión de funciones . Entenderemos convergencias de estas en los siguientes términos:

Convergencia en probabilidad: si

Convergencia en media de orden r:

Convergencia en ley o en distribución:

cuando esto ocurre diremos que se distribuye asintóticamente como X,

Ejemplo1: Sea la sucesión de variables aleatorias , donde sigue una distribución de Bernoulli de parámetro . Comprobar que converge en probabilidad, en media de orden r y en ley hacia 0 (variable aleatoria 0).

Solución

Ley débil de los grandes números (Teorema de Khinchin): Sea una sucesión de variables aleatorias independientes y con la misma distribución, entonces

Un caso particular en la Ley de regularidad estadística, que afirma que la frecuencia relativa de un suceso A, fr(A), tiende hacia la probabilidad del mismo, p(A)

Basta definir como 1 si ocurre A y 0 en otro caso.

 

Otro caso particular que se desprende es el que afirma que la función de distribución empírica tiende hacia la teórica

 

Quizá el resultado más significativo que se deduce es que los momentos muestrales convergen en probabilidad hacia los poblacionales, en concreto, y para los estadísticos habituales:

 

Teorema del límite central (de Levy-Lindeberg)

Sea una sucesión de variables aleatorias independientes y con la misma distribución, entonces

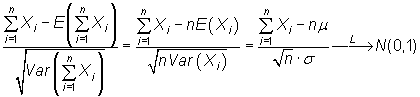de donde deducimos la distribución asintótica de la media y de la suma, esto es,

  

Fue Moivre, en 1733, quien primero proporcionó una versión del teorema sólo para variables de Bernoulli con equiprobabilidad. Laplace lo generalizó para cualquier probabilidad. Lyapunoff, en 1901, da la primera demostración rigurosa del resultado.

Para variables independientes e igualmente distribuidas, Levy y Lindeberg lo prueban 20 años después. Finalmente, Lyapunov probó una versión para variables independientes que cumplan cierta condición.

Observemos que en el caso que la variable tenga una distribución normal, coincide la distribución exacta y la asintótica.

En concreto, y para alguna de las variables habituales

Puede comprobarse la convergencia en la siguiente hoja de cálculo

Ejemplo 1:

Sea la sucesión de variables aleatorias , donde sigue una distribución de Bernoulli de parámetro . Comprobar que converge en probabilidad, en media de orden r y en ley hacia 0 (variable aleatoria 0).

La variable es

El suceso coincide con , cuya probabilidad es y al tomar límite es nulo.

En este caso , y el límite es de nuevo 0.

Después, comprobaremos que el límite funcional de la primera es la segunda. En efecto, la función de distribución de es:

y la de es

Es inmediato que el límite cuando n tiende a infinito de la primera es la segunda, por tanto, se tiene la convergencia en ley o en distribución.

La función de distribución empírica

El objetivo de la función de distribución empírica es construir una distribución de frecuencias acumuladas para una cierta realización muestral.

Así, disponemos de una m.a.s. de una variable aleatoria X y disponemos de su realización muestral .

A continuación, ordenamos dicha realización que será un resultado de la muestra ordenada .

La construcción de esta función de distribución es:

Es decir, utilizando la muestra ordenada

o también puede expresarse como , donde expresa la función indicador, esto es, la función de distribución empírica coincide con la frecuencia de los valores .

El aspecto de esta función es el de una distribución escalonada (discreta).

Si hay empates, esto es, caso que varias variables de la muestra ordenada coincidieran, entonces el valor de la función de distribución empírica se incrementaría proporcionalmente al número de empates. (Ver ejemplo)

Fijar la atención sobre el caracter aleatorio de esta función. Se trata, en definitiva, de una variable aleatoria discreta que para cada número real x toma los valores . En concreto se tiene que el número de variables de la muestra que son menores o iguales que x es una distribución binomial, así

Si repetimos sucesivamente el experimento la función de distribución empírica se aproxima (converge en probabilidad) a la función de distribución teórica. Es decir,

Este resultado será utilizado posteriormente para evaluar lo acertado de la muestra o de si está "demasiado" alejada de la población, estudiándolo a través del estadístico , que evaluará su diferencia.

Ejemplo 2.- Sea una variable aleatoria con distribución uniforme en el intervalo (4,5), es decir, con función de densidad,

Planteamos extraer una m.a.s. de tamaño 8 de ella, dibujar la distribución empírica y compararla con la teórica. En segundo lugar, repetir la experiencia con varias muestras más del mismo tamaño y observar su "aspecto". Por último, observar que si extraemos una muestra de mayor tamaño, 1000, la distribución empírica se aproxima más a la teórica. Todo ello en una hoja de cálculo.