proviene
de una población con distribución de Bernoulli b(p), entonces
se tiene que su suma, 
, sigue
una distribución B(n,p). El muestreo en proporciones.
Si la muestra proviene
de una población con distribución de Bernoulli b(p), entonces
se tiene que su suma, , sigue
una distribución B(n,p).
Si n es suficientemente grande entonces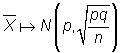 
,
luego tipificando queda:
 |
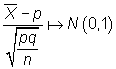El denominador se llama error estándar de la proporción muestral y decrece al crecer el tamaño de la muestra.
Si disponemos de dos poblaciones, una de tamaño 
y otra
de tamaño 
y
se pretende comparar cierta proporción (
y
) en ambas,
asumiendo que son independientes se tiene
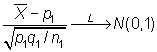y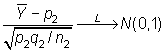 
y al tratarse de dos normales pueden restarse, con lo que tendremos
un estadístico que incluye la diferencia de las proporciones y :
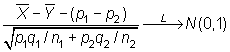
Ejemplo 1: Lanzamos una moneda 5 veces (¿o 5 monedas una vez?, reflexiona sobre la igualdad de resultados). Obtener el muestreo aleatorio con reposición y sin reposición de las monedas, calculando en cada uno de los casos la distribución de los principales estadísticos.
