MEDIDAS DE POSICIÓN

Las medidas de posición más habituales son: la esperanza, la mediana y la moda. Otras medidas que también se utilizan son los cuantiles.

- La Esperanza Matemática

La esperanza matemática o media teórica de una distribución es el principal resumen de una variable aleatoria.

Bajo ciertas condiciones (dispersión pequeña) esta medida es un buen resumen de la distribución de probabilidad.

Si X es una v.a. discreta que toma los valores y es su función de probabilidad entonces su esperanza se define a partir de la siguiente suma

Si X es una v.a. continua y es su función de densidad entonces se define su esperanza a partir de la siguiente integral:

Ejemplos de la esperanza de una variable discreta y de una continua puede verse en o en , por ejemplo.

Además, podemos calcular directamente la esperanza de cualquier función de una variable aleatoria. Así, si X es una v.a. y g(X) es una v.a. función de X, la esperanza de g(X) se obtiene como

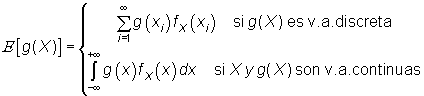Propiedades de la esperanza:

1. Si X está acotada, , entonces su esperanza existe y .
2. Si entonces
3. Si X es una v.a. no negativa, , y su esperanza existe entonces también será no negativa
4. La esperanza de una constante es la propia constante, .
5. Sean g(X) y h(X) dos funciones v.a. de X existiendo sus respectivas esperanzas entonces En particular:
   • 
   • 
   • 
   • 
   • 
6. Sean g(X) y h(X) dos funciones v.a. de X existiendo sus respectivas esperanzas tales que entonces
7. Si existe la esperanza de X entonces
8. Si la función de probabilidad o densidad de X es simétrica respecto de un valor a, su esperanza, si existe es dicho valor a.
9. Sea Y la v.a. obtenida al aplicar un cambio de origen y de escala a la v.a. X, .Si la esperanza de X existe entonces la de Y también y se verifica que .

- La Mediana y cuantiles

La mediana es otra medida de posición central que proporciona aquél valor que deja la mitad de la probabilidad a la izquierda y la mitad a la derecha.

En general, si X es una v.a. la mediana es cualquier valor que verifica

y

En particular, si X es continua las anteriores condiciones se simplifican y la mediana es cualquier valor que verifica

De la misma forma, se definen otras medidas de posición denominados cuantiles. Así, el cuantil de orden q es cualquier valor que verifica:

y

es decir, cualquier valor que deja a la izquierda una probabilidad (al menos) q y el resto a su derecha. Análogamente, si X es continua el cuantil de orden q , es cualquier valor que verifica .

La mediana en realidad es el cuantil de orden q=0.5.

- La Moda

Es otra medida de posición central que se define como el valor (o valores) de la variable en el que la función de probabilidad (en el caso discreto) o la de densidad (en el caso continuo) alcanza el máximo absoluto.

Las tres medidas de centralización vistas guardan la siguiente relación