 |
Variable cuantitativa frente a variable cuantitativa
El objetivo, en principio, es detectar posibles relaciones lineales entre
las variables (Análisis de correlación) y, si éstas presentan
un fuerte grado de correlación, buscar la forma funcional que mejor
explique la variable dependiente a partir de la independiente (Análisis
de regresión).
Así, podríamos estudiar, por ejemplo, si existe relación
entre la renta y el consumo de las familias y, de existir, tratar de encontrar
la mejor relación funcional que explique el consumo a partir de la renta.
Denotaremos por X e Y a las variables y por a los N pares de valores correspondientes
a los N individuos de la población.
Tablas de contingencia. No tienen interés salvo en el caso, poco
habitual, de que las variables sean “muy discretas”, es decir,
que tomen pocos valores y repetidos.
Representaciones gráficas
Histograma de frecuencias tridimensional. Representación gráfica
de la distribución
conjunta de dos variables cuantitativas agrupados en intervalos de igual
amplitud. A cada par de categorías le corresponde un prisma rectangular
de altura igual a su frecuencia conjunta.
Diagrama de dispersión. En
un sistema de ejes cartesianos se representan los pares de puntos de las dos
variables
analizadas (la variable independiente en abcisas y la variable dependiente
en ordenadas). La forma de la nube de puntos puede dar una idea de la posible
relación funcional entre las variables.
 |
Análisis de correlación. Consiste en obtener una serie de estadísticos que miden el grado de correlación lineal entre las variables. El coeficiente de Pearson utiliza directamente los valores de las variables, mientras que los coeficientes de Spearman y Kendall utilizan los rangos de las mismas. Las tres medidas admiten una interpretación probabilística.
Coeficiente de correlación de Pearson
![]() ,
,
donde![]() es la covarianza entre X e Y,
es la covarianza entre X e Y,
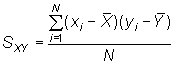
y ![]() y
y ![]() sus
respectivas desviaciones. Es decir,
sus
respectivas desviaciones. Es decir,
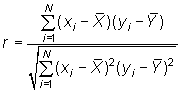 .
.
El coeficiente está comprendido entre –1 y 1: valores próximos
a 1 revelan relaciones más o menos lineales y crecientes; valores próximos
a –1, relaciones más o menos lineales y decrecientes; por último,
valores próximos a 0, ausencia de relación lineal (r =
0, X e
Y están incorrelacionadas). Los siguientes gráficos
ilustran las
distintas situaciones.
Coeficiente de correlación de rangos de Spearman
Si denotamos por X’ e Y’ los rangos (el número
de orden de sus valores) de X y de Y, el coeficiente de correlación de rangos
de Spearman es el coeficiente de correlación de Pearson para X’ e
Y’:
![]() .
.
La medida se interpreta en el mismo sentido que el coeficiente de Pearson, pero en este caso en términos de rangos.
Coeficiente de concordancia de Kendall
Sean X e Y las variables que recogen las clasificaciones de los individuos
respecto de dos conceptos, en principio sin empates. Para cada par de valores
, se contabiliza el número de pares, , para los que las dos variables
están en el mismo sentido (concordancias) y el número de pares
en sentido inverso (discordancias). Así,
![]() e
e ![]() son
concordantes si
son
concordantes si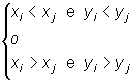
![]() e
e ![]() son
discordantes si
son
discordantes si 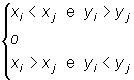
Entonces, el coeficiente tau de Kendall se define como
![]()
donde C y D denotan el número de
pares concordantes y discordantes, respectivamente.
La medida está comprendida entre –1 y 1: si está próximo
a 1 las dos clasificaciones son más o menos concordantes; si está próximo
a –1, son más o menos discordantes; por último, si está próximo
a 0, las dos clasificaciones no guardan relación.
Análisis de regresión
El análisis de regresión tiene por objetivo, en principio,
obtener la función matemática que mejor explica una variable
cuantitativa Y (variable dependiente o a explicar) a partir de otra variable
cuantitativa X (variable independiente o explicativa); posteriormente,
el análisis de regresión se extiende pudiéndose explicar
una variable (o más), cuantitativa o, incluso, cualitativa, a partir
de varias variables cuantitativas y cualitativas.
Además de la finalidad explicativa, el análisis de regresión
permitirá predecir valores de la variable dependiente para distintos valores
de la independiente.
Así, se trataría de explicar Y mediante f(X),
función
de X que se aproxima a Y pero no coincide con Y (las
relaciones entre variables no son exactas):
![]() .
.
Dicha función es la estimación de Y, ![]() ,
,
![]()
cometiéndose errores pues Y y su estimación no tienen porqué coincidir en todos sus puntos:
![]() .
.
Más en concreto, para cada par de valores correspondiente a uno de los N individuos, se obtiene
![]()
![]()
La función f se puede buscar sin ningún
tipo de limitación
(regresión general de escaso interés práctico) o limitándose
a algún tipo de función sencilla (lineal, ![]() ,
parabólica
de 2º grado,
,
parabólica
de 2º grado, ![]() ,
exponencial,
,
exponencial, ![]() o
o ![]() ,…).
El caso más común es el de regresión lineal; diversos
motivos avalan esta elección:
,…).
El caso más común es el de regresión lineal; diversos
motivos avalan esta elección:
- La relación más o menos lineal entre variables es frecuente;
en muchas situaciones en las que no se da originalmente esta relación,
ciertas transformaciones sencillas en las variables (transformaciones logarítmicas,
exponenciales, inversas, cuadráticas,...) permiten obtener la deseada
linealidad.
- La relación lineal es fácilmente interpretable.
- Los desarrollos matemáticos se facilitan.
Entonces:
![]()
![]()
De entre todas las posibles rectas, buscaremos aquella que produzca menos errores; en concreto, obtendremos aquella que minimice la suma de los errores al cuadrado:
![]()
Los valores de a y b que minimizan la suma de los errores al cuadrado,
![]() (ordenada
en el origen)
(ordenada
en el origen)
![]() (pendiente)
(pendiente)
dan lugar a la recta de regresión mínimo cuadrática.
El coeficiente a nos da el valor de Y cuando X es cero (no es siempre interpretable)
mientras que b es lo que crece o decrece
Y cuando X crece en una unidad.
Para valorar la bondad de la recta de regresión tenemos en cuenta la
descomposición de la varianza,
![]() ,
,
esto es,
Variabilidad total o a explicar = Variabilidad de la regresión + Variabilidad residual o no explicada |
A partir de aquí se define el coeficiente de determinación,
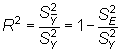 ,
,
la variabilidad explicada sobre la variabilidad a explicar (habitualmente en
porcentaje), que permite evaluar la capacidad explicativa y predictiva del
modelo propuesto.
Cuando la regresión es lineal y sólo se dispone de una variable
explicativa,
![]() ,
,
esto es, el coeficiente de determinación (mide la bondad del ajuste lineal) es igual al cuadrado del coeficiente de correlación de Pearson (mide la intensidad y el sentido de la relación lineal).
En la hoja adjunta se muestra un ejemplo en el que se aplica esta técnica de análisis bivariante.
En algunas ocasiones, los valores de las variables pueden
agruparse en intervalos y aplicar
las técnicas de análisis de dependencia vistas
para dos características cualitativas. Véase ejemplo.