Concepto y construcción

La estimación puntual presenta un gran inconveniente: aún utilizando el mejor estimador de una característica poblacional o parámetro, no sólo no acertaremos en la estimación (la posibilidad de acertar es remota), sino que desconoceremos el grado de precisión y fiabilidad de la misma. Así, cuando estimamos que el número medio de horas diarias ante el televisor es 2.3 a partir de la información que proporcionan 1000 individuos elegidos al azar, no medimos ni la discrepancia con el verdadero valor del parámetro (precisión), ni la probabilidad de equivocarse en menos de una cierta cantidad (fiabilidad). La única garantía que podemos tener acerca de la bondad de la estimación proviene del hecho de que se ha realizado con el estimador más adecuado (en ese caso, la media muestral). Para evitar esta insuficiencia de la estimación puntual se introducen los intervalos de confianza.

Conceptos

Un ejemplo

Tamaño muestral, precisión y fiabilidad

De manera más formal, dada una muestra aleatoria simple y dos estadísticos, y, tal que , es un intervalo de confianza aleatorio para el parámetro a nivel 1- si

Para una realización de la muestra, , obtenemos el intervalo de confianza numérico:

El nivel de confianza, 1-, mide la fiabilidad del intervalo de probabilidad, esto es, la probabilidad de acertar. Habitualmente se toman valores como 0.90, 0.95 o 0.99, correspondientes a valores de de 0.10, 0.05 y 0.01, probabilidad de equivocarse.

Mientras consideremos la muestra como aleatoria interpretaremos el intervalo en términos de probabilidad. Una vez concretados los valores de la muestra y, por tanto, del intervalo, interpretaremos éste en términos de confianza: si pudiésemos repetir la toma de datos de forma reiterada, el de los intervalos contendría el verdadero valor del parámetro. La hoja adjunta ilustra este hecho a partir de 150 intervalos de confianza sobre la media poblacional obtenidos simulando una misma distribución normal.

La longitud del intervalo, , mide la precisión de la estimación: intervalos largos proporcionan estimaciones imprecisas, mientras que intervalos cortos proporcionan estimaciones precisas. Habitualmente la precisión se expresa como el radio del intervalo, , el margen de error de la estimación.

Un intervalo de confianza puede utilizarse para tomar decisiones sobre el verdadero valor del parámetro. Así, planteada una hipótesis sobre , , se acepta (no se rechaza) si es uno de los valores del intervalo.

Un ejemplo nos ayudará a construir un intervalo y a entender los principales conceptos. Queremos saber acerca del número de horas diarias de estudio de los bachilleres españoles, para lo cual tomamos una muestra de tamaño 1000 que arroja los resultados que se incluyen en la tabla:

siendo 2.7 el número medio de horas diarias que dedican al estudio los 1000 bachilleres seleccionados. La figura muestra el histograma de frecuencias de estos datos.

Vamos a construir el intervalo de confianza para la media de horas diarias de estudio de los bachilleres, , a un nivel de confianza de 0.95, esto es, con una probabilidad de equivocarnos de 0.05.

Para abordar el problema suponemos que X, número de horas de estudio diarias de un bachiller, sigue una distribución normal de media , desconocida, y de varianza 0.81. La suposición de normalidad está plenamente justificada dada la naturaleza de la variable, que se ve influida por múltiples factores; esta suposición se ve corroborada por la forma que presenta el histograma anterior, que no es muy diferente a la función de densidad de una normal. Por otro lado, la suposición de varianza conocida carece de fundamento (si la media es desconocida, con más motivo lo será también la varianza), pero esta suposición sirve para introducir el problema sin excesivas complicaciones formales. Por tanto,

La media muestral, , el mejor estimador de , es de nuevo la clave para encontrar un intervalo de confianza sobre a nivel de confianza de 1- . Para construir el intervalo de confianza, necesitamos conocer la distribución del estadístico . La media muestral de una muestra aleatoria simple de tamaño n de una variable normal, , tiene una distribución normal de media y de varianza :

Este resultado permite construir un intervalo de confianza sobre cuando suponemos conocida . Para ello, tipifiquemos previamente el estimador , restándole la media y dividiendo por su desviación, trasformación ésta que no afecta a su normalidad:

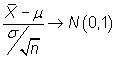A partir de este resultado, que proporciona el estadístico pivote, buscamos dos valores y tales que dejen entre sí una probabilidad de 1- en una distribución normal tipificada. De esta forma,

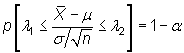En esta doble desigualdad operamos para dejar sólo y en el centro de la misma el parámetro , objetivo de nuestra inferencia. Así se obtiene un intervalo de confianza para a nivel 1- :

Notemos que existen muchas parejas que dejan entre ellas una probabilidad de 1- pero, evidentemente, es deseable que la estimación sea lo más precisa posible, esto es, que el intervalo tenga longitud mínima. En este caso, la longitud del intervalo es

longitud que se hace mínima cuando y estén lo más cerca posible, situación que se da cuando son simétricos. Entonces, a y los denotaremos como y . De esta forma, el intervalo óptimo (el más corto) es

En concreto, para construir un intervalo de confianza al 95% sobre el número medio de horas de estudio, , con una muestra de tamaño 1000, sustituyendo se obtiene:

donde –1.96 y +1.96 son los dos puntos que en la distribución normal estándar dejan 0.025 de probabilidad en cada cola. Simplificando resulta

lo que permite decir que el verdadero valor del parámetro está entre y , con una probabilidad de 0.95, o lo que es lo mismo, que el verdadero valor de difiere de la media muestral en, a lo sumo, 0.056 con una probabilidad de 0.95. Como se ve, estos dos estadísticos son estimadores por defecto y por exceso, respectivamente, de .

Finalmente, dado que el número medio de horas de estudio entre los bachilleres de la muestra era 2.7, se sustituye en la anterior expresión dando lugar al intervalo real

pudiéndose afirmar con una confianza del 95% que el número medio de horas diarias dedicadas al estudio de los bachilleres españoles está entre 2.64 y 2.75.

Obsérvese que este intervalo no puede interpretarse en términos de probabilidad, sino en términos de confianza. Si hemos acertado, está entre dichos valores, y si hemos fallado, no está entre los mismos, pero nunca sabremos en cuál de las dos situaciones nos encontramos. Si este problema se plantea repetidas veces tomando cada vez una muestra distinta, obtendríamos intervalos de confianza no aleatorios y distintos en cada caso, pudiéndose afirmar que en el 95% de esos intervalos hemos acertado, y que en el 5% restante hemos fallado (nunca podremos identificar cuáles son aquéllos en los que hemos acertado y aquéllos en los que hemos fallado).

Véase en la hoja adjunta el intervalo aquí construido.

Adviértase que en la construcción del intervalo de confianza podemos controlar tres factores:

• El tamaño de la muestra n que nos cuantifica el número de observaciones y, por tanto, la cantidad de información de que dispondremos.
• La fiabilidad del intervalo, 1- , esto es, la probabilidad de que el parámetro se encuentre dentro del intervalo aleatorio; o lo que es lo mismo, la probabilidad de equivocarse, .
• La precisión de la estimación o longitud del intervalo, L.

Así, en el intervalo construido, contábamos con una muestra de tamaño 1000 y para una fiabilidad de 0.95 hemos obtenido un intervalo de longitud 0.12, o en notación más habitual, con una precisión de +/-0.06.

Fijado uno de los tres factores anteriores podemos ver cómo se relacionan los otros dos entre sí. Desarrollemos estos resultados en el supuesto del ejemplo planteado, si bien todas las conclusiones son generalizables a cualquier otra situación.

I.- Fijado el tamaño de la muestra, n, una mayor fiabilidad (es decir, menor ) implica una menor precisión (un intervalo más largo); esto es, si queremos incrementar la probabilidad de acierto lo haremos a expensas de perder precisión en la estimación.

La longitud del intervalo de confianza óptimo para la media poblacional de una variable normal con desviación conocida vale:

Entonces, fijado el tamaño n, al crecer (menor fiabilidad), decrece, para dejar a su derecha una cola más grande, y L también decrece (mayor precisión). Por tanto, la longitud del intervalo es función decreciente de . Compruébese este hecho en la hoja adjunta obteniendo un intervalo con una mayor fiabilidad, en concreto, al 99%.

Todo esto nos confirma la imposibilidad de encontrar un intervalo ideal, muy fiable y muy preciso, teniendo que llegar a situaciones de compromiso en las que no se sacrifique la precisión para conseguir una fiabilidad óptima y viceversa.

II.- Para una fiabilidad concreta, un aumento en el tamaño de la muestra, produce una mejora en la precisión de la estimación. Esto es, si es fijo, al aumentar el tamaño muestral n, la longitud L del intervalo decrece, hecho que se deduce a partir de la expresión de la longitud del intervalo:

Compruébese este hecho en la hoja adjunta, construyendo para una muestra de tamaño 100 el intervalo de confianza al 95%.

III.- Para una precisión fijada, un aumento en el tamaño muestral, produce una mayor fiabilidad.

De la expresión de la longitud del intervalo deducimos que

Entonces, si L permanece fijo, un aumento de n produce un aumento de , o lo que es lo mismo, una disminución en la probabilidad . Por tanto, si pretendemos que el intervalo tenga una longitud determinada y podemos aumentar el tamaño de la muestra, este aumento provoca una mayor fiabilidad en la estimación ( disminuye).

Estas dos últimas observaciones evidencian un resultado totalmente esperable: la posibilidad de contar con una muestra más grande mejora la estimación, bien sea aumentando la fiabilidad (disminuyendo ), bien sea aumentando la precisión (disminuyendo L).

Ahora bien, este deseable aumento de información no siempre es posible. Pensemos que una muestra más grande supone un mayor coste económico, una mayor demora en la obtención de resultados e, incluso, una pérdida en la calidad de la información. En la práctica, el cliente que encarga una encuesta a un estadístico le pide que los resultados obtenidos tengan una cierta fiabilidad (un determinado 1- ) y una cierta precisión (un determinado L); el estadístico determinará una muestra lo más pequeña posible (esto es, lo más barata, rápida y buena posible) para conseguir dichos objetivos (con todo esta situación no deja de ser ideal pues en la mayor parte de las situaciones el cliente dispondrá de un techo presupuestario lo que limitará el número de observaciones a realizar). En esta situación, despejando n en la expresión de la longitud del intervalo, se obtiene:

de donde podremos obtener el valor de n que nos proporcione un intervalo de confianza de una fiabilidad y una precisión determinada.

En la hoja adjunta se muestra los tamaños muestrales para distintas precisiones y fiabilidades; asimismo permite calcular uno de los tres factores ( tamaño, fiabilidad o precisión) a partir de los otros dos.

Por último, la varianza juega también un papel importante en la estimación por intervalos. En concreto, las variables menos dispersas (menos variables), es decir, las que tienen varianza pequeña, admiten una mejor estimación, en el sentido de una estimación más fiable y precisa. Compruébese este hecho en la hoja adjunta aumentando o disminuyendo el valor de la desviación poblacional.