Distribución de una variable aleatoria

Una variable aleatoria se caracteriza por su distribución, es decir, por el reparto de las probabilidades entre todos los valores que tome. Esta distribución se puede representar mediante dos funciones que asignan probabilidad (de diferente forma) a los valores que toma la variable:

• Función de distribución.
• Función de probabilidad o función de densidad.

Función de distribución

Se define la función de distribución de una variable X en un punto x como:

Esta función en el punto x acumula toda la probabilidad asignada a todos los valores de la variable que se encuentran dentro del intervalo .

Propiedades de la función de distribución:

1. Es una función monótona creciente (va acumulando probabilidad)
2. Es una función continua por la derecha
3. Verifica que y , es decir, asíntotas en cero y uno.

Además es una función acotada entre 0 y 1 y caracteriza completamente a la variable.

En concreto, si X es una variable discreta su función de distribución es escalonada con saltos en los valores que toma la variable (ver ejemplo) y si X es una variable continua entonces su función de distribución es siempre continua (ver ejemplo).

Función de probabilidad

Si X es una variable aleatoria discreta se define su función de probabilidad en un punto x como:

Esta función en el punto x toma la probabilidad del valor x.

Es decir, si X es una variable que toma valores en su función de probabilidad es:

• si
• si

  Ejemplo: en la gráfica apreciamos una variable discreta que toma 6 valores con probabilidad 1/6 cada uno (lo que llamaremos uniforme discreta)

Propiedades de la función de probabilidad de una variable discreta:

1. Es una función acotada :
2. La suma es la unidad, .

Además si conocemos la función de probabilidad podemos obtener la función de distribución y viceversa de la siguiente manera:

• 
• 

  Ejemplo: en la gráfica apreciamos la función en escalera (la distribución) de la variable discreta anterior, superpuesta con la función de probabilidad

Función de densidad

Si X es una variable aleatoria continua entonces su función de distribución es una función continua y derivable y su derivada es continua (salvo, alo sumo, en un número finito de puntos) y se define su función de densidad en un punto x como:

Propiedades de la función de densidad:

1. Es una función positiva:
2. Su integral es la unidad

Además si conocemos la función de densidad podemos obtener la función de distribución y viceversa de la siguiente manera:

• por ser la función de densidad la derivada de la función de distribución.
• 

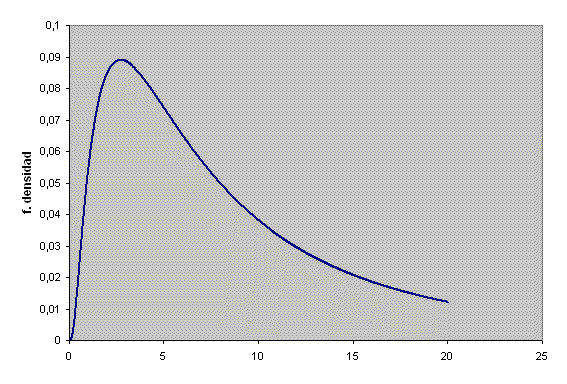
  Ejemplo: la gráfica muestra una función de densidad

Cálculo de probabilidades mediante la función de distribución

Conocida la función de distribución de la variable aleatoria X, podemos deducir interesantes propiedades que nos permiten calcular la probabilidad de cualquier suceso a partir de dicha función, así por ejemplo tenemos,

donde y son los límites por la izquierda, es decir, y

Además cualquier otro intervalo real probabilizable se puede escribir como uniones o intersecciones (en una cantidad numerable) de intervalos del anterior tipo, por tanto aplicando las propiedades de la probabilidad se obtendría la probabilidad de cualquier suceso real.

Vamos a concretar el cálculo de las anteriores probabilidades dependiendo si estamos trabajando con una variable discreta o continua.

• Variables discretas

En el caso de que X sea una variable aleatoria discreta tomando valores sabemos que los únicos puntos donde se acumula probabilidad (probabilidad estrictamente positiva) es precisamente en dichos valores (saltos en la función de distribución). Supongamos además que a,b se encuentran en la siguiente posición:

Entonces se tiene que , , y que . Sustituyendo en las expresiones anteriores se obtiene la probabilidad de cualquier intervalo.

• Variables continuas

Por otro lado, si X es una variable aleatoria continua, su función de distribución es una función continua por tanto, y el cálculo de probabilidades en los intervalos cerrados [a,b], en los abiertos (a,b) o en los semiabiertos [a,b) y (a,b] es el mismo:

Cálculo de probabilidades mediante la función de probabilidad

Sea X es una variable aleatoria discreta con valores y tales que,

también se puede obtener la probabilidad de cualquier intervalo real a partir de la función de probabilidad de la siguiente manera:

Cálculo de probabilidades mediante la función de densidad

Análogamente, si X es una variable aleatoria continua y se conoce su función de densidad, también podemos calcular cualquier probabilidad a partir de ella, así tenemos,