Estimadores suficientes
Decimos que un estimador es suficiente cuando es suficiente
como estadístico, esto es, cuando tiene tanta información sobre el parámetro
como la propia muestra. Más en concreto,
Sea 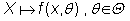 una
población, y una
población, y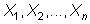 una
m.a.s. de X. Decimos que un estimador, una
m.a.s. de X. Decimos que un estimador, 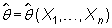 de q, es suficiente para el parámetro
si la densidad o función de probabilidad de la muestra condicionada
por un valor cualquiera del estimador,
de q, es suficiente para el parámetro
si la densidad o función de probabilidad de la muestra condicionada
por un valor cualquiera del estimador,
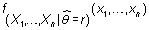
no depende del parámetro.
|
Las propiedades de los estimadores suficientes resultan de
recordar las de los estadísticos suficientes. En concreto, la obtención de
estimadores suficientes se realiza a través del criterio de factorización,
que enunciamos aquí para estimadores:
Recuérdese que esta factorización debe realizarse para todo
punto 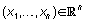 y todo
valor del parámetro
y todo
valor del parámetro 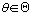 ,
lo que ocasiona dificultades cuando el campo de variación de la muestra depende
del parámetro.
,
lo que ocasiona dificultades cuando el campo de variación de la muestra depende
del parámetro.
El Ejemplo3 ilustra este concepto.
Puedes ver otras ilustraciones en la continuación
del Ejemplo1 o en la continuación
del Ejemplo2.
![]() una
población, y
una
población, y![]() una
m.a.s. de X. Decimos que un estimador,
una
m.a.s. de X. Decimos que un estimador, ![]() de q, es suficiente para el parámetro
si la densidad o función de probabilidad de la muestra condicionada
por un valor cualquiera del estimador,
de q, es suficiente para el parámetro
si la densidad o función de probabilidad de la muestra condicionada
por un valor cualquiera del estimador,![]()