Contrastes en poblaciones normales
Una población
En la inferencia sobre una variable numérica en una población, el objetivo principal de los test de hipótesis es contrastar el valor de alguna medida de posición (media o mediana), de dispersión (varianza) o de algún otro parámetro poblacional. Así, si se cuenta con información muestral sobre el número de horas diarias que un individuo está viendo la televisión, trataremos de ver si podemos aceptar que el promedio de horas en la población toma un determinado valor.
En principio, si hacemos
inferencia sobre un resumen de la variable podemos considerar que dicha variable
sigue una distribución y plantear el problema desde la óptica
paramétrica. Esa distribución puede ser cualquiera de las muchas
distribuciones tipo (binomial, Poisson, normal, uniforme, gamma,...). Ahora
bien, por distintos motivos (variables, originales o transformadas, con distribución
más o menos campaniforme, teorema del límite central, simplicidad
en los procedimientos, ...), lo más habitual es la suposición
de normalidad. Entonces, suponiendo que la variable X sigue una
distribución normal de media ![]() y
desviación
y
desviación ![]() ,
plantearemos contrastes de hipótesis sobre dichos parámetros.
,
plantearemos contrastes de hipótesis sobre dichos parámetros.
En la inferencia sobre dos
variables numéricas en una población se trata de
ver si existe relación
lineal entre las mismas a partir de la información muestral.
Así, podemos tratar de analizar si existe relación entre la
renta y el consumo de las familias y cuál es la intensidad y el sentido
de la misma, concretándose la inferencia en el coeficiente de correlación
![]() .
Este tipo de análisis, denominado genéricamente
de correlación, conduce de forma inmediata al análisis de regresión:
si existe relación trataremos de encontrar la función que mejor
exprese esta relación.
.
Este tipo de análisis, denominado genéricamente
de correlación, conduce de forma inmediata al análisis de regresión:
si existe relación trataremos de encontrar la función que mejor
exprese esta relación.
Dos poblaciones
En este caso, el objetivo fundamental es
comparar la distribución de una variable cuantitativa X en
las dos poblaciones (subpoblaciones) determinadas por las modalidades de una
característica cualitativa dicotómica o, lo que es lo mismo,
estudiar si la variable cuantitativa (variable respuesta) presenta diferencias
significativas en cada uno de los dos niveles de la variable cualitativa (factor).
Esta comparación se realizará a partir de la información
parcial que proporcionan dos muestras. Denotaremos por ![]() y
y ![]() a
la variable cuantitativa en cada una de las dos situaciones.
a
la variable cuantitativa en cada una de las dos situaciones.
Si podemos aceptar normalidad, el objetivo general de comparar dos poblaciones se traduce en comparar las medias de la variable en cada una de ellas; aunque suele tener únicamente un interés instrumental, también se pueden comparar las varianzas.
Para poder realizar estas comparaciones se utilizan dos muestras provenientes de individuos diferentes (estudiar las posibles diferencias salariales en función del sexo a partir de una muestra de hombres y una muestra de mujeres); en este caso hablaremos de muestras independientes. A veces se puede utilizar una muestra con los mismos individuos para las dos situaciones de la variable (comparar la valoración de dos detergentes a partir de los datos que sobre uno y otro proporciona una única muestra de consumidores); en este caso hablaremos de muestras apareadas o relacionadas. Siempre que se puedan considerar muestras relacionadas, este procedimiento proporciona en principio mejores inferencias.
El problema de comparar medias se puede generalizar a más de dos poblaciones, los llamados procedimientos ANOVA.
| Poblaciones normales | Una población | Una variable | C. de H. sobre la media poblacional |
| C. de H. sobre la varianza poblacional | |||
| Dos variables | C. de H. sobre el coeficiente de correlación poblacional | ||
| Dos poblaciones | Muestras independientes | C. de H. sobre la diferencia de medias poblacionales | |
| C. de H. sobre el cociente de varianzas poblacionales | |||
| Muestras relacionadas | C. de H. sobre la diferencia de medias poblacionales | ||
Contrastes de hipótesis sobre la media poblacional
Sea X una variable con distribución
normal de media ![]() y desviación
y desviación ![]() y
una muestra de tamaño n,
y
una muestra de tamaño n, ![]() :
:
A partir del estadístico
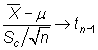 |
se pueden construir los siguientes contrastes
de hipótesis a nivel de significación ![]() :
:
a) Bilateral
Teniendo en cuenta el estadístico
bajo ![]() ,
se rechaza esta hipótesis
cuando
,
se rechaza esta hipótesis
cuando
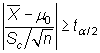 |
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
El estadístico mide la discrepancia
entre la media muestral, observada o empírica, ![]() ,
y la media poblacional, esperada o teórica
bajo
,
y la media poblacional, esperada o teórica
bajo ![]() ,
, ![]() :
discrepancias significativamente grandes llevan a rechazar
:
discrepancias significativamente grandes llevan a rechazar ![]() .
.
Además,
siendo ![]() el
valor muestral del estadístico.
el
valor muestral del estadístico.
b) Unilateral
Se rechaza ![]() cuando
cuando
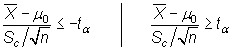 |
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
Además,
En la hoja adjunta se muestra un ejemplo de estos contrastes.
Cuando la variable X no es normal, pero el tamaño muestral es suficientemente grande, en base al teorema del límite central se pueden aplicar los anteriores contrastes, que en este caso serían aproximados.
Contrastes de hipótesis sobre la varianza poblacional
Sea X una variable con distribución
normal de media ![]() y
desviación
y
desviación ![]() y
una muestra de tamaño n,
y
una muestra de tamaño n, ![]() :
:
A partir del estadístico
se pueden construir los siguientes contrastes
de hipótesis a nivel de significación ![]() :
:
a) Bilateral
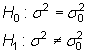 |
Teniendo en cuenta el estadístico
bajo ![]() ,
se rechaza esta hipótesis
cuando
,
se rechaza esta hipótesis
cuando
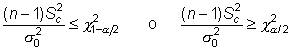 |
siendo ![]() y
y ![]() los
valores que en una distribución
los
valores que en una distribución ![]() con n-1
grados de libertad
dejan a su derecha una probabilidad de
con n-1
grados de libertad
dejan a su derecha una probabilidad de ![]() y
y
![]() , respectivamente.
, respectivamente.
Además,
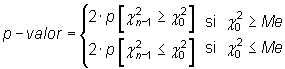 |
donde ![]() es
el valor muestral del estadístico y Me la mediana de la distribución.
es
el valor muestral del estadístico y Me la mediana de la distribución.
b) Unilateral
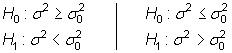 |
Se rechaza ![]() cuando:
cuando:
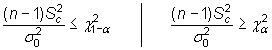 |
siendo ![]() y
y ![]() los
valores que en una distribución
los
valores que en una distribución ![]() con n-1
grados de libertad
dejan a su derecha una probabilidad de
con n-1
grados de libertad
dejan a su derecha una probabilidad de ![]() y
y
![]() ,
respectivamente.
,
respectivamente.
Además,
En la hoja adjunta se muestra un ejemplo de estos contrastes.
El estadístico utilizado en estos contrastes exige una normalidad estricta en la variable.
Contrastes de hipótesis sobre la diferencia de medias poblacionales
Sean ![]() y
y ![]() variables
normales, de media
variables
normales, de media ![]() y
y ![]() y
de varianza
y
de varianza ![]() y
y ![]() , respectivamente,
e independientes, disponiéndose de sendas muestras
aleatorias de tamaño
, respectivamente,
e independientes, disponiéndose de sendas muestras
aleatorias de tamaño ![]() y
y ![]() :
:
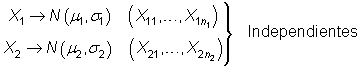 |
A partir del estadístico
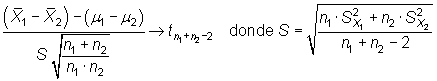 |
si las varianzas se pueden suponer iguales, y del estadístico
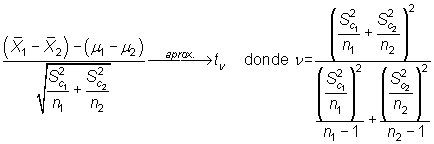 |
en caso contrario, se pueden construir los siguientes contrastes
de hipótesis a nivel de significación ![]() :
:
Bilateral
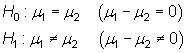 |
Teniendo en cuenta el estadístico bajo ![]() ,
se rechaza esta hipótesis
cuando
,
se rechaza esta hipótesis
cuando
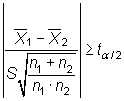 |
o cuando
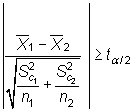 |
dependiendo de si podemos suponer las varianzas
iguales o no. En ambos casos,
![]() es
el valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
es
el valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
Los estadísticos miden
la discrepancia entre la diferencia de medias muestrales, observadas o empíricas, ![]() ,
y la diferencia de medias poblacionales, esperadas o teóricas bajo
,
y la diferencia de medias poblacionales, esperadas o teóricas bajo ![]() ,
, ![]() :
discrepancias significativamente grandes llevan a rechazar
:
discrepancias significativamente grandes llevan a rechazar ![]() .
.
Además,
siendo ![]() el
valor muestral del correspondiente estadístico y m los
grados de libertad de la correspondiente distribución t de Student.
el
valor muestral del correspondiente estadístico y m los
grados de libertad de la correspondiente distribución t de Student.
En el mismo sentido que este contraste de diferencia de medias igual a cero (igualdad de medias), se pueden construir contrastes de diferencia de medias igual a d.
El test admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de estos contrastes.
Cuando las variables ![]() y
y ![]() no
son normales,
pero los tamaños muestrales son suficientemente grandes, en base al
teorema del límite central se pueden aplicar los anteriores contrastes,
que en este caso serían aproximados.
no
son normales,
pero los tamaños muestrales son suficientemente grandes, en base al
teorema del límite central se pueden aplicar los anteriores contrastes,
que en este caso serían aproximados.
Contrastes de hipótesis sobre el cociente de varianzas poblacionales
Sean ![]() y
y ![]() variables
normales, de media
variables
normales, de media ![]() y
y ![]() y
de varianza
y
de varianza ![]() y
y ![]() ,
respectivamente, e independientes, disponiéndose de sendas muestras
aleatorias de tamaño
,
respectivamente, e independientes, disponiéndose de sendas muestras
aleatorias de tamaño ![]() y
y ![]() :
:
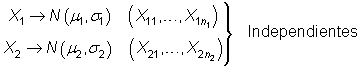 |
A partir del estadístico
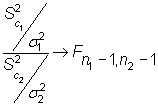 |
se pueden construir los
siguientes contrastes
de hipótesis a nivel de significación ![]() :
:
Bilateral
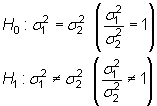 |
Teniendo en cuenta el estadístico
bajo ![]() , se rechaza
esta hipótesis cuando
, se rechaza
esta hipótesis cuando
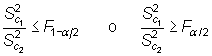 |
siendo ![]() y
y ![]() los
valores que en una distribución F con
los
valores que en una distribución F con
![]() y
y ![]() grados
de libertad dejan a su derecha una probabilidad de
grados
de libertad dejan a su derecha una probabilidad de ![]() y
y ![]() ,
respectivamente.
,
respectivamente.
Además,
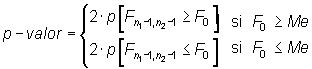 |
donde ![]() es
el valor muestral del estadístico y Me la mediana de la distribución.
es
el valor muestral del estadístico y Me la mediana de la distribución.
En el mismo sentido que este contraste de cociente de varianzas igual a uno (igualdad de varianzas), se pueden construir contrastes de cociente de varianzas igual a c.
La elección de uno u otro estadístico para contrastar o estimar por intervalo la diferencia de medias se realiza a partir del resultado del contraste previo de igualdad de varianzas.
El test admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de estos contrastes.
El estadístico utilizado en estos contrastes exige una normalidad estricta en las variables.
Contrastes de hipótesis sobre la diferencia de medias poblacionales
Sean ![]() y
y ![]() variables,
de media
variables,
de media ![]() y
y ![]() ,
respectivamente, disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Entonces se puede
considerar la variable
,
respectivamente, disponiéndose de sendas muestras aleatorias de tamaño n relativas
a los mismos individuos (o individuos gemelos). Entonces se puede
considerar la variable ![]() ,
de la que se dispone de una muestra aleatoria simple,
,
de la que se dispone de una muestra aleatoria simple, ![]() ,
donde
,
donde ![]() , variable
que se supone normal de media
, variable
que se supone normal de media ![]() y
de varianza
y
de varianza ![]() :
:
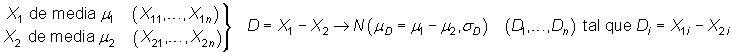 |
A partir del estadístico
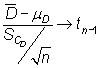 |
se pueden construir los siguientes contrastes
de hipótesis a nivel de significación ![]() :
:
Bilateral
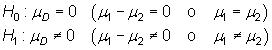 |
Teniendo en cuenta el estadístico
bajo ![]() , se rechaza
esta hipótesis cuando
, se rechaza
esta hipótesis cuando
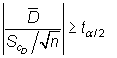 |
siendo ![]() el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de
el
valor que en una distribución t de Student con n-1 grados
de libertad deja a su derecha una probabilidad de ![]() .
.
El estadístico mide la discrepancia
entre la diferencia de medias muestrales, observadas o empíricas, ![]() ,
y la diferencia de medias poblacionales, esperadas o teóricas bajo
,
y la diferencia de medias poblacionales, esperadas o teóricas bajo ![]() ,
, ![]() :
discrepancias significativamente grandes llevan a rechazar
:
discrepancias significativamente grandes llevan a rechazar ![]() .
.
Además,
siendo ![]() el
valor muestral del estadístico.
el
valor muestral del estadístico.
El test admite planteamiento unilateral.
En la hoja adjunta se muestra un ejemplo de estos contrastes.
Cuando la variable D no es normal, pero el tamaño muestral es suficientemente grande, en base al teorema del límite central se pueden aplicar los anteriores contrastes, que en este caso serían aproximados.
Contraste de hipótesis sobre el coeficiente
de correlación
lineal de Pearson
Sea (X,Y) una variable con
distribución
normal bidimensional cuyo coeficiente de correlación es ![]() ,
,
siendo ![]() ,
, ![]() y
y ![]() la
covarianza y las desviaciones típicas
poblacionales, disponiéndose de una muestra de tamaño n,
la
covarianza y las desviaciones típicas
poblacionales, disponiéndose de una muestra de tamaño n,
![]() .
.
A partir del estadístico Z de Fisher,
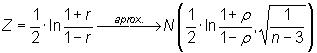 |
se obtiene el correspondiente intervalo de confianza,
así como contrastes
de hipótesis. Ahora bien, este estadístico permite
construir contrastes sobre ![]() para
cualquier valor de la prueba, pero dado que nuestro interés se va
a centrar en el cero (
para
cualquier valor de la prueba, pero dado que nuestro interés se va
a centrar en el cero (![]() ,
incorrelación), se facilitan los cálculos utilizando
el estadístico
,
incorrelación), se facilitan los cálculos utilizando
el estadístico
siendo esta distribución válida
sólo cuando ![]() .
.
A partir de este estadístico se
pueden construir los siguientes contrastes de hipótesis a nivel de
significación ![]() :
:
a) Bilateral
Teniendo en cuenta el estadístico
bajo ![]() , se
rechaza esta hipótesis cuando
, se
rechaza esta hipótesis cuando
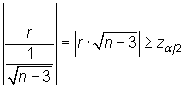 |
siendo ![]() el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de
el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de ![]() .
.
Además,
siendo ![]() el
valor muestral del estadístico.
el
valor muestral del estadístico.
b) Unilateral
Se rechaza ![]() si
si
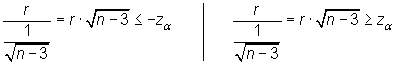 |
siendo ![]() el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de
el
valor que en una distribución normal estándar deja a su derecha
una probabilidad de ![]() .
.
Además,
En la hoja adjunta se muestra un ejemplo de estos contrastes.
Cuando la variable (X,Y) no es normal, pero el tamaño muestral es suficientemente grande, en base al teorema del límite central se pueden aplicar los anteriores contrastes, que en este caso serían aproximados.