DISTRIBUCIONES UNIDIMENSIONALES DISCRETAS

Uniforme discreta

La distribución rectangular, también llamada uniforme discreta, es la de una variable aleatoria, X, que tome la misma probabilidad para N valores igualmente espaciados entre dos valores, a y b (a<b). Su función de probabilidad vale

para , siendo h el espacio entre dos valores consecutivos, .

Haciendo el cambio se obtiene la forma estándar, que toma los valores 1,2,...,N con la misma probabilidad.

X	Forma estándar

Obviamente, todos los valores son modas. En cuanto a la Mediana

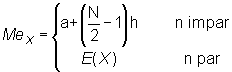Los coeficientes de simetría (skewness) y aplastamiento (kurtosis) se obtienen a partir de los anteriores momentos,

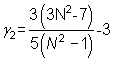Ejemplo 1: El clásico del lanzamiento de un dado de seis caras equiprobable, esto es, cada lado tiene la misma probabilidad de salir que cualquier otro.

 

Bernoulli:

Cuando el interés reside no en saber cuál es el resultado de un experimento concreto sino si éste ha ocurrido o no. A eso se conoce como experimento de Bernoulli.

En un experimento de Bernoulli se denomina éxito al suceso en estudio, A, y fracaso a su contrario, . A este suceso le asociamos la variable aleatoria, X, definida como el número de éxitos al realizar el experimento. Es decir,

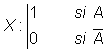
Llamamos p=p(A), a la probabilidad de éxito y q=1-p=p() a la probabilidad de fracaso.

Se denota como y su función de probabilidad es

y su función de distribución

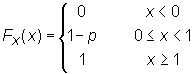
Finalmente:

Ejemplo 2: Sea el experimento de Bernoulli consistente en lanzar un tiro libre a una canasta de baloncesto por parte de un jugador. El éxito es encestar y el fracaso no encestar. Del historial deportivo del jugador se sabe que encesta el 80% de las veces, entonces, asociamos al experimento la variable de Bernoulli, número de aciertos al realizar un tiro libre, cuya distribución es

Es decir, la variable X tiene una distribución b(0.8).

Distribución Binomial:

La distribución binomial fue presentada y obtenida por J. Bernoulli en 1713, simbólicamente se representa por B(n,p), y se define como el número de éxitos en n tiradas de Bernoulli independientes, siendo p la probabilidad de éxito en cada tirada.

Para n=1 la distribución se denomina de Bernoulli, abreviadamente b(p). De hecho, la binomial es una suma de variables independientes de Bernoulli.

Su función de probabilidad, para , es

Su esperanza vale E[X]=n·p, y su varianza, Var(X)=n·p·(1-p).

La moda es

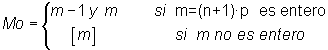
donde [m] expresa la parte entera de m.

El coeficiente de asimetría es y el de curtosis .

Un resultado de interés es también:

Cuando n>20, su función de distribución puede aproximarse por la de una normal, de media np y varianza npq.

Ejemplo 3: El jugador de baloncesto lanza una serie de 5 tiros libres. Calcular la probabilidad de que enceste dos. ¿Y de que enceste al menos 3?

En este caso la variable X es el número de encestes, de 5 intentos, sigue una distribución B(5,0.8). Con lo cual, la probabilidad de sólo dos encestes de 5 intentos es:

Por su parte, la probabilidad de al menos 3 encestes es

Esta probabilidad puede calcularse directamente, o bien buscando en tablas tabuladas, o bien puedes buscar en la hoja de cálculo , introducir los valores de los parámetros, n=5, p=0.8 y el valor de k=3. La hoja devolverá el valor tabulado.

Distribución de Poisson:

Históricamente, la distribución de Poisson aparece como límite de la distribución binomial cuando el número de experimentos tiende a infinito y la probabilidad de éxito tiende hacia cero.

Simbólicamente se describe como P(l), aparece como aproximación a la distribución binomial, B(n,p), cuando n es grande y p pequeño, siendo E(X)=l=Var(X).

Su función de probabilidad es

Admite una única moda cuando l no es entero (la moda es la parte entera de l, [l]) y dos cuando es entero (l-1y l).

Su coeficiente de asimetría vale , y el de curtosis .

Si l>20 su función de distribución se aproxima a una normal de la misma media y varianza.

Ejemplo 4: El jugador de baloncesto tiene una media de 1 enceste por temporada desde una distancia de 10 metros. Admitiendo que el número de enceste desde esa distancia sigue una distribución de Poisson, ¿cuál es la probabilidad de que consiga dos encestes?, y ¿la probabilidad de más de 3 encestes?

En este caso X, número de canastas desde una distancia de 10 metros, sigue una P(1) (ya que 1=E(X)), entonces se pide

La segunda probabilidad es p[X>3], que resulta

.

Como en el ejemplo anterior, la probabilidad podría calcularse directamente, o bien buscando en tablas tabuladas, o bien puedes con ayuda de la hoja de cálculo , introducir los valores del parámetro, l=1 y el valor de k=3. La hoja devolverá el valor tabulado.

Distribución geométrica:

La distribución geométrica, simbólicamente descrita como G(p), describe las probabilidades de obtener k fracasos antes del primer éxito, al realizar sucesivas tiradas de Bernoulli independientes, con probabilidad p de éxito.

Su función de probabilidad es

Su función de distribución vale , para k=0,1,... lo que facilita el cálculo de cuantiles.

Su esperanza vale , y su varianza .

La moda vale siempre 0.

El coeficiente de simetría resulta y el de curtosis .

Posee una importante propiedad llamada "del olvido", o de la falta de memoria.

Ejemplo 5: Para el jugador de baloncesto al lanzar tiros libres, ¿cuál es el número medio de fallos antes del primer acierto?

La variable de estudio es ahora, X, número de tiros libres fallados antes del primer enceste. Es decir, se trata de una geométrica de parámetro 0.8, G(0.8), con lo cual el número medio de fallos antes del primer acierto es la esperanza de la misma, es decir,

Distribución binomial negativa:

La distribución binomial negativa, simbólicamente descrita como BN(r,p), describe las probabilidades de obtener k fracasos antes del r-ésimo éxito, al realizar sucesivas tiradas de Bernoulli independientes, con probabilidad p de éxito.

Su función de probabilidad es

Su esperanza vale , y su varianza .

Para r=1 coincide con la distribución geométrica.

El coeficiente de simetría vale , y el de curtosis, .

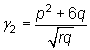La Binomial negativa es una suma de variables geométricas de parámetro p, independientes

Ejemplo 6: Para el jugador de baloncesto, ¿cuál es la probabilidad de que falle 5 tiros libres antes de conseguir 7 puntos?

En este caso la variable X es número de canastas falladas antes del 7º acierto, es decir, se trata de una BN(7,0.8), con lo cual, la probabilidad pedida es:

Distribución hipergeométrica:

La distribución hipergeométrica proporciona probabilidades de extraer k bolas blancas de una urna en la que hay N1 blancas y N2 negras (N=N1+N2), en n extracciones sin reposición.

Cuando hay reposición se obtiene la distribución binomial B(n,p), con p=N1/N. De hecho, si N>50 y n/N<=0.1, se acepta que coinciden.

La función de probabilidad es

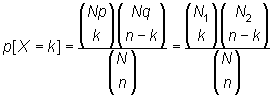para máx(0,n-N2)<=k<=mín(n,N1).

Su esperanza coincide con la de la binomial, E[X]=n·p, pero la varianza es menor, .

Ejemplo 7: En el equipo hay 8 jugadores que lo hacen en el puesto de alero, dos de los cuales son extranjeros. El entrenador selecciona a dos de ellos para el 5 inicial, ¿cuál es la probabilidad de que uno de ellos sea extranjero?

Ahora la variable X es el número de jugadores extranjeros elegidos. Dicha variable sigue una H(8,2,0.25), con lo que la probabilidad de que uno sea extranjero es del 42.8%:

Volver