DISTRIBUCIONES UNIDIMENSIONALES CONTINUAS

Distribución Uniforme continua:

La distribución uniforme continua U(a,b), es la de una variable aleatoria, X, con valores en el intervalo (a,b) y para las que la probabilidad de un intervalo es proporcional a su longitud, sea cual sea su posición.

Su función de densidad es constante,

y su función de distribución lineal,

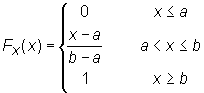Despejando, se obtienen los cuantiles, qr=a+r(b-a) para 0<r<1.

La mediana coincide con la media, Me=(a+b)/2.

La moda es cualquier valor de la variable.

Sus momentos son E[X]=(a+b)/2, Var(X)=(b-a)2/12, g1=0 y g2=-6/5.

Si X sigue una U(a,b), entonces

Además:

Este resultado será de gran importancia cuando estudiemos la simulación de variables.

Ejemplo 1: En un trayecto urbano hay dos semáforos consecutivos de modo que 2.5 minutos después de que el primero se ponga verde se pone rojo el segundo. Ambos se cierran cada 2 minutos, permaneciendo cerrados 30 segundos.

Un conductor se ha detenido en el primero y el tiempo en recorren la distancia entre ambos semáforos es una U(1,4). ¿Cuál es la probabilidad de que se pare en el segundo?

Del enunciado se deduce que deberá parar si emplea entre 2.5 y 3 minutos en ir del primero al segundo, es decir,

p[2.5 < X < 3]= F(3) - F(2.5) = (3-1) / 3 - (2.5-1) / 3 = 0.166.

Distribución Normal:

La distribución normal es la primera distribución continua que se estudia sistemáticamente y, desde luego, la más ampliamente utilizada. Abreviadamente se describe como N(m,s), donde m es la esperanza y s >0 la desviación típica. Su función de densidad vale

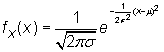Su moda y mediana coinciden con la esperanza, Me=Mo = m=E(X) .

Cuando m=0 y s=1 se añade el adjetivo "estándar".

Parte de su importancia deriva del hecho de que el promedio de variables aleatorias independientes y equidistribuidas se distribuye aproximadamente como una distribución normal.

Se utiliza también ampliamente en la contrastación de hipótesis estadísticas y en la construcción de intervalos de confianza.

Su coeficiente de simetría vale g1=0 (simétrica) y su curtosis es estándar, ya que g2=0 (mesocúrtica).

Un hecho que simplifica el cálculo de probabilidades es

La suma de variables independientes normales, también es normal. De hecho se tiene:

Sean variables aleatorias independientes con . Dados los números reales entonces

Sean variables aleatorias independientes e igualmente distribuidas con distribución N(m,s). Entonces la media muestral

Ejemplo 2: El diámetro interior de ciertas piezas sigue una distribución normal de media 5 y desviación típica 0.5. ¿Qué porcentaje de piezas tiene diámetro superior a 6 centímetros?

Se pide p[X > 6], que es 1- F(6). Ahora bien, para calcular esta probabilidad debo tipificar la variable y buscarlo en las tablas de la normal estándar o puede buscarlo en la hoja de cálculo , especificando la media 5, la desviación 0.5 y el valor x=6, que me devuelve que la probabilidad acumulada hasta él es 0.97725, de donde la probabailidad pedida es

p[X > 6] = 0.02275.

Distribución Lognormal:

La distribución log-normal, propuesta por Galton en 1879, es la exponencial de una variable normal.

Así, si Y es N(m,s), X=exp[Y] es log-normal, descrita abreviadamente como logN(m,s). Su función de densidad vale

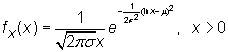Momentos:

Esperanza
Varianza
Moda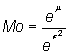
Mediana

Ejemplo 3: Los ingresos de los habitantes de un municipio siguen una distribución logarítmico normal de parámetros 3 y 2. ¿Qué porcentaje de individuos se encuentra entre 70 y 150?

La variable X sigue una LN(3,2), se pide entonces,

Esto es, el 10.89% de los individuos de ese municipio tienen ingresos entre 70 y 150.

Distribución Gamma:

La distribución gamma (Laplace, 1836) es una distribución biparamétrica, que se designa abreviadamente como g(a,p), donde a y p son valores positivos. Su función de densidad vale

donde . Además,

Esperanza
Varianza
Moda	si p>1
Mediana	carece de expresión explícita
Coeficiente de simetría
Coeficiente de Kurtosis

En particular: Dos distribuciones gamma son especialmente utilizadas: la denominada chi-2 con n grados de libertad (g(1/2 , n/2)), y la exponencial negativa (g(a,1)) .

• La suma de variables gamma g (a,p) independientes es una variable gamma de primer parámetro a y de segundo parámetro la suma de todos los segundos parámetros.
• Si X es una g (a,p), entonces k X es una g (a / k , p)

  Ejemplo 4: El tiempo de reparación, en horas, de una pieza es una g (0.5 , 2). El precio de venta de la misma es de 5 mil euros y el de fabricación de mil euros. ¿A cuanto debemos cobrar la hora de reparación para obtener un beneficio medio de 3 mil euros?

  Se nos pide una cantidad K, de modo que el beneficio medio, E(B), sea 3.

  El beneficio es B=5- (K X +1), entonces, E(B)= 4 - K* E(X) = 4 - K* (2 / 0.5) lo igualamos a 3, de donde se deduce que K=1/4, es decir 250 euros, para obtener un beneficio de 3 mil euros.

Distribución Exponencial negativa:

Es una caso particular de la Gamma cuando p=1. E (a)= g (a,1)

Función de densidad	Función de distribución
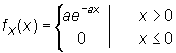E(X)= 1 / a

La suma de variables exponenciales independientes es una gamma.

Tiene la propiedad del olvido, es decir cumple que

Ejemplo 5: El tiempo en servir una mercancía es una E (a) de media 5. Han pasado 2 días y el cliente aún no ha recibido la mercancía, ¿cuál es la probabilidad de que tenga que esperar al menos 3 días más?

Como E(X)=5, el parámetro en 1/5.

Debemos calcular p[ X > 5 | X > 2 ] = p [ X > 3 ] = 0.606.

Distribución Beta:

La distribución beta, abreviadamente b(A,B,p,q)(p>0,q>0), tiene por función de densidad

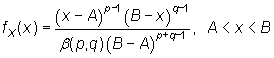donde , es la denominada función beta.

Para A=0 y B=1 se obtiene su forma estándar, descrita como b(0,1,p,q) o b(p,q) (no confundir con la función beta), con función de densidad

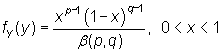Claramente, si X es una b(A,B,p,q) e Y una beta estándar, X=A+(B-A)Y.

Momentos: y

Si p>1 y q>1, .

La mediana no tiene una expresión explícita, debiendo calcularse por procedimientos aproximados.

Su coeficiente de simetría vale y el de curtosis, .

Ejemplo 6: La proporción media de tubos defectuosos es del 20%. Dicha proporción se modeliza como una b(p,8). Calcular p.

Sabemos que E(X)=0.2 = p / (p+8), de donde p=2.

Distribución de Pareto:

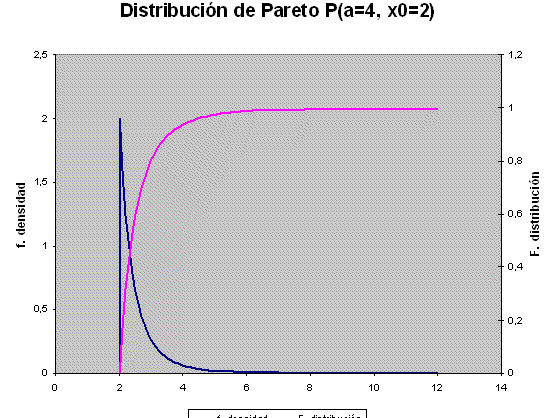
La distribución de Pareto (Pareto, 1897) propuesta por este autor como ley "universal" de distribución de la renta en una población, es una distribución biparamétrica: a es el parámetro de forma y x0 es la renta mínima. Su función de densidad es

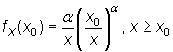y la de distribución

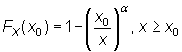La moda vale x0 y la mediana .

El r-cuantil resulta .

Los momentos se obtienen con facilidad observando que , de donde se obtiene y .

Ejemplo 7: Sea X una variable con distribución de Pareto(a, x0). Calcular su coeficiente de variación y la mediana.

Conocemos las expresiones de la media y de la varianza, por lo que , observemos que dicho coeficiente no depende del segundo parámetro, sólo lo hace de a.

Para la mediana, se tiene que , de donde resulta que .

Distribución Logística:

La curva logística es una función real de variable real y aparece originariamente descrita en un tratado de Verhulst en1845 aparece como curva adecuada para describir el crecimiento de poblaciones y, en general, en los procesos de crecimiento que experimentan estados de saturación. Aplicada al estudio de la distribución de la recta, de la mortalidad, del crecimiento poblacional, etc.

Una variable aleatoria logística, X, con parámetros a y b (abreviadamente L(a,b)), es aquélla cuya función de distribución sigue una curva logística,

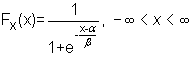Su función de densidad vale

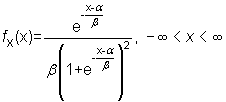Haciendo el cambio se obtiene la distribución logística estándar, L(0,1).

Como puede verse en la hoja de cálculo, se parece a la distribución normal de la misma esperanza y varianza, si bien las colas y el centro están algo más levantados.

Su esperanza vale E[X]=a, y su varianza, . La moda y la mediana son también iguales al parámetro a.

Su coeficiente de simetría vale g1=0 (simétrica) y el de curtosis, g2=1.2 (leptocúrtica).

Distribución de Weibull:

La distribución de Weibull (Weibull, 1939) es una distribución triparamétrica, abreviadamente descrita como W(x0,b,a), con función de densidad

y de distribución

Propuesta inicialmente para estudiar la resistencia de los materiales a la rotura, hoy día se emplea en Control de calidad y en fiabilidad de sistemas.

La variable es una exponencial negativa de parámetro 1, e(1).

Existe una distribución de Weibull estándar, W(0,1,a).

Los momentos de X se obtienen sin dificultad a partir de los de Y.