Método de máxima verosimilitud

Como el ejemplo anterior ilustra, una posibilidad prudente, cuando se desea una estimación puntual de un parámetro, consiste en elegir como estimación el valor del parámetro que maximiza la función de verosimilitud (dicho valor del parámetro será una función de porque la función de verosimilitud depende de la realización de la muestra). Si esta maximización la obtenemos para una realización cualquiera, dispondremos de la expresión del estimador, que se denomina máximo-verosímil. Formalicemos el resultado.

• Por el aspecto de la función de verosimilitud, suele ser más fácil maximizar su neperiano que la propia función. Formalmente, este criterio de trabajo es perfectamente correcto, ya que, como la verosimilitud es no negativa, para obtener el máximo basta con trabajar donde es estrictamente positiva (el máximo no se encontrará nunca donde la verosimilitud es igual a cero), con lo que el neperiano de la función de verosimilitud está definido en el campo de interés.

  Esta práctica es tan habitual que se utiliza una notación específica para dicho logaritmo, que a veces se denomina log-verosimilitud. Se escribe como o, de forma más abreviada, como . En concreto,

• Asimismo, la versimilitud (y su neperiano) suelen ser derivables como funciones del parámetro, por lo que una buena práctica inicial consiste tratar de maximizar la función utilizando las condiciones relacionadas con las derivadas, esto es, primera derivada nula y segunda negativa. Esquemáticamente,

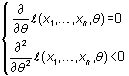
Con frecuencia, esta práctica proporciona el máximo o, al menos, indicaciones acerca de cómo obtenerlo. La primera de estas dos condiciones (anulación de la primera derivada) recibe el nombre de ecuación de verosimilitud.

Los siguientes ejemplos muestran cómo se desarrollan los cálculos analíticamente.

Anteriormente estudiábamos la función de verosimilitud para una población de Bernoulli en el Ejemplo3. En la continuación del Ejemplo 3 veremos la estimación máximo verosímil del parámetro. Pueden verse otros ejemplos en la continuación del Ejemplo 1 o en la continuación del Ejemplo 2

El libro VEROSI.XLS muestra la dinámica de la máxima verosimilitud.

Máxima verosimilitud para varios parámetros

El método de máxima verosimilitud se aplica de la misma manera si hay más de un parámetro a estimar, si bien con una mayor complejidad en el cálculo del máximo. La idea es totalmente similar:

Ilustraremos el procedimiento con la estimación de los dos parámetros, m y (nótese que consideramos , y no s como parámetro, por lo que las funciones se escriben en función de y con respecto al mismo se toman las derivadas) de una población normal. La verosimilitud resulta

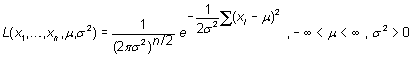
y su neperiano

La ecuación de verosimilitud es ahora un sistema de dos ecuaciones con dos incógnitas,

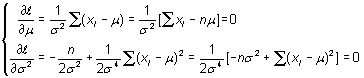
De la primera se obtiene , que sustituida en la segunda proporciona , esto es,.

La matriz hessiana, sustituidos los parámetros por las soluciones de la ecuación de verosimilitud, resulta

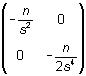
que claramente es definida negativa. En definitiva, los estimadores máximo verosímiles son y .

Máxima verosimilitud e información parcial. Principio de máxima verosimilitud.

La idea que subyace al principio de la estimación máximo-verosímil (maximizar la probabilidad o la densidad de la realización de la muestra) se aplica también cuando no se conoce completamente la realización de la muestra, sino sólamente se dispone de información parcial sobre la misma. Esa información es un suceso, cuya probabilidad dependerá del parámetro; su maximización me proporcionará la estimación máximo verosímil. Resumimos esta idea en un enunciado:

Puede verse una ilustración de esta idea en el Ejemplo 4 o en la continuación del Ejemplo1.

Propiedades de los estimadores máximo-verosímiles

La popularidad del uso de los estimadores máximo-verosímiles se basa en que es un buen estimador del parámetro. Enunciaremos, sin demostrar, sus principales propiedades. En todas ellas supondremos que se dispone de una población, , y que es una muestra aleatoria simple de X

Como puede verse, la propiedad de invariancia permite realizar la estimación máximo-verosímil en el terreno en que nos sea más cómodo. Veamos la siguiente ilustración en la continuación del Ejemplo1.

Aunque sea función de T, esto no quiere decir que sea suficiente, porque la función que los relaciona no tiene por qué ser biyectiva. No obstante, habitualmente lo es, lo que implica que muchas veces el estimador máximo verosímil es efectivamente un estimador suficiente.

La anterior propiedad garantiza que, si hay un estimador eficiente (que de existir es único, como sabemos), el máximo verosímil es eficiente. Para ello se exige, claro está, que se cumplan las condiciones de regularidad de Cramér-Rao, porque de no ser así no podríamos hablar de estimadores eficientes; pero se exige también que el estimador máximo verosímil se obtenga por técnicas de derivación.

Obsérvese, en primer lugar, que las condiciones que se exigen son las mismas que las que garantizan la eficiencia del estimador, cuando existe. Además, se exigen ciertas condiciones de regularidad funcional que se cumplen en los casos que nosotros estudiamos, por lo que no las detallamos.

En cuanto a las conclusiones, obsérvese que, por la primera, se garantiza la consistencia del estimador.

Por la segunda, se obtiene la normalidad como distribución aproximada del estimador máximo-verosímil, lo que permitirá su uso para construir intervalos de confianza aproximados para q. Pero, además, nótese que tiene aproximadamente esperanza nula y varianza unidad, por lo que

o, dicho de otra forma, la esperanza del estimador es aproximadamente igual al parámetro, y además,

o equivalentemente , esto es, la varianza del estimador es aproximadamente la cota de Cramér-Rao. En definitiva, estos resultados se describen diciendo que, en las condiciones del resultado anterior, el estimador máximo verosímil es asintóticamente insesgado y asintóticamente eficiente.